Advertisements
Advertisements
प्रश्न
A beacon makes one revolution every 10 seconds. It is located on a ship which is anchored 5 km from a straight shoreline. How fast is the beam moving along the shoreline when it makes an angle of 45° with the shore?
उत्तर
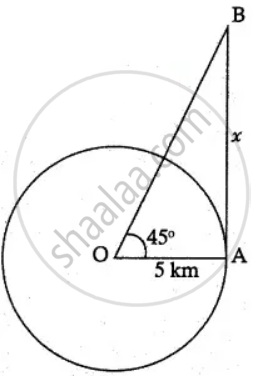
Time for one revolution = 10 sec
Now, angular velocity `"dv"/"dt" = (2pi)/10 = pi/5`
From the figure, tan 45° = `"AB"/"OA"`
1 = `x/5`
⇒ x = 5
Again, tan θ = `x/5`
x = 5 tan θ
Differentiating w.r.t. ‘t’
`("d"x)/"dt" = 5 sec^2theta ("d"theta)/"dt"`
= `5 sec^2 (45^circ) (pi/5)`
= `(sqrt(2))^2pi`
= 2π
∴ The beam is moving at the rate of 2π km/sec.
APPEARS IN
संबंधित प्रश्न
A camera is accidentally knocked off an edge of a cliff 400 ft high. The camera falls a distance of s = 16t2 in t seconds. What is the instantaneous velocity of the camera when it hits the ground?
A particle moves along a line according to the law s(t) = 2t3 – 9t2 + 12t – 4, where t ≥ 0. At what times the particle changes direction?
A particle moves along a line according to the law s(t) = 2t3 – 9t2 + 12t – 4, where t ≥ 0. Find the total distance travelled by the particle in the first 4 seconds
If the volume of a cube of side length x is v = x3. Find the rate of change of the volume with respect to x when x = 5 units
A stone is dropped into a pond causing ripples in the form of concentric circles. The radius r of the outer ripple is increasing at a constant rate at 2 cm per second. When the radius is 5 cm find the rate of changing of the total area of the disturbed water?
A conical water tank with vertex down of 12 metres height has a radius of 5 metres at the top. If water flows into the tank at a rate 10 cubic m/min, how fast is the depth of the water increases when the water is 8 metres deep?
A ladder 17 metre long is leaning against the wall. The base of the ladder is pulled away from the wall at a rate of 5 m/s. When the base of the ladder is 8 metres from the wall. How fast is the top of the ladder moving down the wall?
Find the points on curve y = x3 – 6x2 + x + 3 where the normal is parallel to the line x + y = 1729
Find the tangent and normal to the following curves at the given points on the curve
y = x2 – x4 at (1, 0)
Find the tangent and normal to the following curves at the given points on the curve
y = x4 + 2ex at (0, 2)
Find the equations of the tangents to the curve y = 1 + x3 for which the tangent is orthogonal with the line x + 12y = 12
Choose the correct alternative:
The volume of a sphere is increasing in volume at the rate of 3π cm3/ sec. The rate of change of its radius when radius is `1/2` cm
Choose the correct alternative:
A balloon rises straight up at 10 m/s. An observer is 40 m away from the spot where the balloon left the ground. The rate of change of the balloon’s angle of elevation in radian per second when the balloon is 30 metres above the ground
Choose the correct alternative:
The position of a particle moving along a horizontal line of any time t is given by s(t) = 3t2 – 2t – 8. The time at which the particle is at rest is
Choose the correct alternative:
Find the point on the curve 6y = x3 + 2 at which y-coordinate changes 8 times as fast as x-coordinate is
Choose the correct alternative:
The slope of the line normal to the curve f(x) = 2 cos 4x at x = `pi/12` is
Choose the correct alternative:
The tangent to the curve y2 – xy + 9 = 0 is vertical when
Choose the correct alternative:
Angle between y2 = x and x2 = y at the origin is
Choose the correct alternative:
The maximum slope of the tangent to the curve y = ex sin x, x ∈ [0, 2π] is at
