Advertisements
Advertisements
प्रश्न
A cricket ball of mass 150 g has an initial velocity `u = (3hati + 4hatj)` m s−1 and a final velocity `v = - (3hati + 4hatj)` m s−1 after being hit. The change in momentum (final momentum-initial momentum) is (in kg m s1)
पर्याय
zero
`-(0.45 hati + 0.6 hatj)`
`-(0.9 hati + 1.2 hatj)`
`-5 (hati + hatj)`
उत्तर
`-(0.9 hati + 1.2 hatj)`
Explanation:
Given, `u = (3hati + 4hatj)` m/s
And `v = - (3hati + 4hatj)` m/s
Mass of the ball = 150 g = 0.15 kg
Δp = Change in momentum
= Final momentum – Initial momentum
= `mv - mu`
= `m(v - u) = (0.15) [- (3hati + 4hatj) - (3hati + 4hatj)]`
= `(0.15) xx [ - 6hati - 8hatj]`
= `- [0.15 xx 6hati + 0.15 xx 8hatj]`
= `- [0.9 hati + 1.20 hatj]`
Hence, Δp = `-[0.9 hati + 1.2 hatj]`
APPEARS IN
संबंधित प्रश्न
The below figure shows the position-time graph of a particle of mass 4 kg.
- What is the force on the particle for t < 0, t > 4 s, 0 < t < 4 s?
- What is the impulse at t = 0 and t = 4 s? (Consider one-dimensional motion only.)

A car accelerates on a horizontal road due to the force exerted by.
A particle of mass 0.3 kg is subjected to a force F = −kx with k = 15 N/m. What will be its initial acceleration if it is released from a point x = 20 cm?
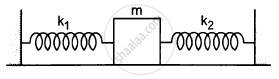
Both the springs shown in the following figure are unstretched. If the block is displaced by a distance x and released, what will be the initial acceleration?
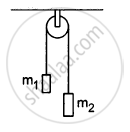
In a simple Atwood machine, two unequal masses m1 and m2 are connected by a string going over a clamped light smooth pulley. In a typical arrangement (In the following figure), m1 = 300 g and m2 = 600 g. The system is released from rest. (a) Find the distance travelled by the first block in the first two seconds; (b) find the tension in the string; (c) find the force exerted by the clamp on the pulley.
A tennis ball and a cricket ball , both are stationary. To start motion in them .
A body of mass 200 g is moving with a velocity of 5 ms−1. If the velocity of the body changes to 17 ms−1, calculate the change in linear momentum of the body.
Define Newton’s second law of motion.
The motion of a particle of mass m is given by x = 0 for t < 0 s, x(t) = A sin 4 pt for 0 < t < (1/4) s (A > o), and x = 0 for t > (1/4) s. Which of the following statements is true?
- The force at t = (1/8) s on the particle is – 16π2 Am.
- The particle is acted upon by on impulse of magnitude 4π2 A m at t = 0 s and t = (1/4) s.
- The particle is not acted upon by any force.
- The particle is not acted upon by a constant force.
- There is no impulse acting on the particle.
Figure shows (x, t), (y, t ) diagram of a particle moving in 2-dimensions.
|
|
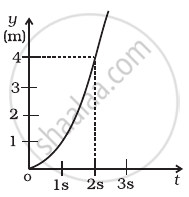 (b) |
If the particle has a mass of 500 g, find the force (direction and magnitude) acting on the particle.