Advertisements
Advertisements
प्रश्न
Both the springs shown in the following figure are unstretched. If the block is displaced by a distance x and released, what will be the initial acceleration?
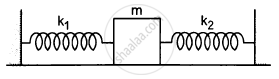
उत्तर
Let the block m be displaced towards left by displacement x.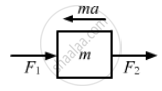
\[\therefore F_1 = -K_1X\] (compressed)
\[ F_2 = -K_2X\] (expanded)
\[ma = F_1 + F_2\]
\[\Rightarrow a = \frac{- x\left( k_1 + k_2 \right)}{m}\]
i.e. \[\left( k_1 + k_2 \right)\frac{x}{m}\] opposite the displacement or towards the mean position.
APPEARS IN
संबंधित प्रश्न
Two bodies of masses 10 kg and 20 kg respectively kept on a smooth, horizontal surface are tied to the ends of a light string. A horizontal force F = 600 N is applied to
- A,
- B along the direction of string. What is the tension in the string in each case?
Explain why a cricketer moves his hands backwards while holding a catch.
An aircraft executes a horizontal loop at a speed of 720 km/h with its wings banked at 15°. What is the radius of the loop?
A block of mass 15 kg is placed on a long trolley. The coefficient of static friction between the block and the trolley is 0.18. The trolley accelerates from rest with 0.5 ms–2 for 20 s and then moves with uniform velocity. Discuss the motion of the block as viewed by (a) a stationary observer on the ground, (b) an observer moving with the trolley.
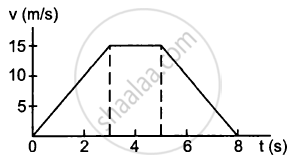
A particle of mass 50 g moves in a straight line. The variation of speed with time is shown in the following figure. Find the force acting on the particle at t = 2, 4 and 6 seconds.
A man has fallen into a ditch of width d and two of his friends are slowly pulling him out using a light rope and two fixed pulleys as shown in the following figure. Show that the force (assumed equal for both the friends) exerted by each friend on the road increases as the man moves up. Find the force when the man is at a depth h.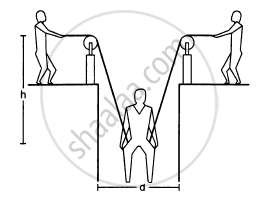
The force of buoyancy exerted by the atmosphere on a balloon is B in the upward direction and remains constant. The force of air resistance on the balloon acts opposite the direction of velocity and is proportional to it. The balloon carries a mass M and is found to fall to the earth's surface with a constant velocity v. How much mass should be removed from the balloon so that it may rise with a constant velocity v?
In the following figure shows a uniform rod of length 30 cm and mass 3.0 kg. The strings shown in the figure are pulled by constant forces of 20 N and 32 N. Find the force exerted by the 20 cm part of the rod on the 10 cm part. All the surfaces are smooth and the strings and the pulleys are light.

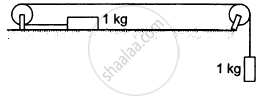
Calculate the tension in the string shown in the following figure. The pulley and the string are light and all the surfaces are frictionless. Take g = 10 m/s2.
Find the acceleration of the blocks A and B in the three situations shown in the following figure.

Two bodies A and B of same mass are moving with velocities v and 2v, respectively. Compare their (i) inertia and (ii) momentum.
A pebble is thrown vertically upwards with a speed of 20 m s-1. How high will it be after 2 s? (Take g = 10 m s-2)
A pebble is dropped freely in a well from its top. It takes 20 s for the pebble to reach the water surface in the well. Taking g = 10 m s-2 and speed of sound = 330 m s-1. Find : The depth of water surface
A stone is thrown vertically upward with a velocity of 9.8 m/s. When will it reach the ground?
A ball is thrown upward and reaches a maximum height of 19.6 m. Find its initial speed?
A hockey player is moving northward and suddenly turns westward with the same speed to avoid an opponent. The force that acts on the player is ______.
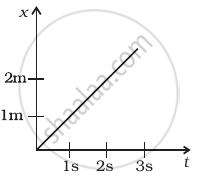
The position time graph of a body of mass 2 kg is as given in figure. What is the impulse on the body at t = 0 s and t = 4 s.

A woman throws an object of mass 500 g with a speed of 25 ms1.
- What is the impulse imparted to the object?
- If the object hits a wall and rebounds with half the original speed, what is the change in momentum of the object?
Figure shows (x, t), (y, t ) diagram of a particle moving in 2-dimensions.
|
|
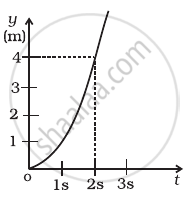 (b) |
If the particle has a mass of 500 g, find the force (direction and magnitude) acting on the particle.