Advertisements
Advertisements
प्रश्न
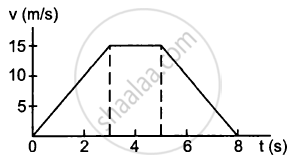
A particle of mass 50 g moves in a straight line. The variation of speed with time is shown in the following figure. Find the force acting on the particle at t = 2, 4 and 6 seconds.
उत्तर
Given:
Mass of the particle, m = 50 g = 5 × 10−2 kg
Slope of the v-t graph gives acceleration.
At t = 2 s,
Slope = \[\frac{15}{3} = 5 m/ s^2\]
So, acceleration, a = 5 m/s2
F = ma = 5 × 10−2 × 5
⇒ F = 0.25 N along the motion.
At t = 4 s,
Slope = 0
So, acceleration, a = 0
⇒ F = 0
At t = 6 sec,
Slope =\[\frac{- 15}{3} = - 5 m/ s^2\]
So, acceleration, a = − 5 m/s2
F = ma = − 5 × 10−2 × 5
⇒ F = − 0.25 N along the motion
or, F = 0.25 N opposite the motion.
APPEARS IN
संबंधित प्रश्न
A man of mass 70 kg stands on a weighing scale in a lift which is moving
- upwards with a uniform speed of 10 m s-1
- downwards with a uniform acceleration of 5 m s–2
- upwards with a uniform acceleration of 5 m s–2. What would be the readings on the scale in each case?
- What would be the reading if the lift mechanism failed and it hurtled down freely under gravity?
Two bodies of masses 10 kg and 20 kg respectively kept on a smooth, horizontal surface are tied to the ends of a light string. A horizontal force F = 600 N is applied to
- A,
- B along the direction of string. What is the tension in the string in each case?
Explain why a cricketer moves his hands backwards while holding a catch.
A smooth wedge A is fitted in a chamber hanging from a fixed ceiling near the earth's surface. A block B placed at the top of the wedge takes time T to slide down the length of the wedge. If the block is placed at the top of the wedge and the cable supporting the chamber is broken at the same instant, the block will.
Two blocks A and B of mass mA and mB , respectively, are kept in contact on a frictionless table. The experimenter pushes block A from behind, so that the blocks accelerate. If block A exerts force F on block B, what is the force exerted by the experimenter on block A?
A force \[\vec{F} = \vec{v} \times \vec{A}\] is exerted on a particle in addition to the force of gravity, where \[\vec{v}\] is the velocity of the particle and \[\vec{A}\] is a constant vector in the horizontal direction. With what minimum speed, a particle of mass m be projected so that it continues to move without being defelected and with a constant velocity?
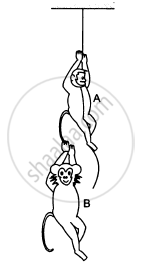
The monkey B, shown in the following figure, is holding on to the tail of monkey A that is climbing up a rope. The masses of monkeys A and B are 5 kg and 2 kg, respectively. If A can tolerate a tension of 30 N in its tail, what force should it apply on the rope in order to carry monkey B with it? Take g = 10 m/s2.
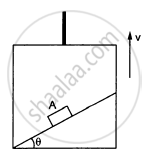
A block A can slide on a frictionless incline of angle θ and length l, kept inside an elevator going up with uniform velocity v in the following figure. Find the time taken by the block to slide down the length of the incline if it is released from the top of the incline.
A force of 10 N acts on a body of mass 2 kg for 3 s, initially at rest. Calculate : Change in momentum of the body.
A bullet of mass 50 g moving with an initial velocity 100 m s-1 strikes a wooden block and comes to rest after penetrating a distance 2 cm in it. Calculate: (i) Initial momentum of the bullet, (ii) Final momentum of the bullet, (iii) Retardation caused by the wooden block and (iv) Resistive force exerted by the wooden block.
A body of mass 200 g is moving with a velocity of 5 ms−1. If the velocity of the body changes to 17 ms−1, calculate the change in linear momentum of the body.
Multiple Choice Question. Select the correct option.
The impulse of a body is equal to:
What do you mean by an impulsive force?
A stone is thrown vertically upward with a velocity of 9.8 m/s. When will it reach the ground?
A ball is thrown upward and reaches a maximum height of 19.6 m. Find its initial speed?
What do you mean by the conservation of momentum? Briefly, explain the collision between two bodies and the conservation of momentum.
A metre scale is moving with uniform velocity. This implies ______.
A cricket ball of mass 150 g has an initial velocity `u = (3hati + 4hatj)` m s−1 and a final velocity `v = - (3hati + 4hatj)` m s−1 after being hit. The change in momentum (final momentum-initial momentum) is (in kg m s1)
The position time graph of a body of mass 2 kg is as given in figure. What is the impulse on the body at t = 0 s and t = 4 s.

