Advertisements
Advertisements
प्रश्न
Two blocks A and B of mass mA and mB , respectively, are kept in contact on a frictionless table. The experimenter pushes block A from behind, so that the blocks accelerate. If block A exerts force F on block B, what is the force exerted by the experimenter on block A?
उत्तर
Let F' = force exerted by the experimenter on block A and F be the force exerted by block A on block B.
Let a be the acceleration produced in the system.
For block A,
\[F' - F = m_A a\] ...(1)
For block B,
F = mBa ...(2)
Dividing equation (1) by (2), we get:
\[\frac{F'}{F} - 1 = \frac{m_A}{m_B}\]
\[\Rightarrow F' = F\left( 1 + \frac{m_A}{m_B} \right)\]
∴ Force exerted by the experimenter on block A is
\[F\left( 1 + \frac{m_A}{m_B} \right)\]
APPEARS IN
संबंधित प्रश्न
Two bodies of masses 10 kg and 20 kg respectively kept on a smooth, horizontal surface are tied to the ends of a light string. A horizontal force F = 600 N is applied to
- A,
- B along the direction of string. What is the tension in the string in each case?
A block of mass m is placed on a smooth wedge of inclination θ. The whole system is accelerated horizontally so that the block does not slip on the wedge. The force exerted by the wedge on the block has a magnitude.
Two objects A and B are thrown upward simultaneously with the same speed. The mass of A is greater than that of B. Suppose the air exerts a constant and equal force of resistance on the two bodies.
A free 238U nucleus kept in a train emits an alpha particle. When the train is stationary, a nucleus decays and a passenger measures that the separation between the alpha particle and the recoiling nucleus becomes x at time t after the decay. If the decay takes place while the train is moving at a uniform velocity v, the distance between the alpha particle and the recoiling nucleus at a time t after the decay, as measured by the passenger, is
car moving at 40 km/hr is to be stopped by applying brakes in the next 4 m. If the car weighs 2000 kg, what average force must be applied to stop it?
A person is standing on a weighing machine placed on the floor of an elevator. The elevator starts going up with some acceleration, moves with uniform velocity for a while and finally decelerates to stop. The maximum and the minimum weights recorded are 72 kg and 60 kg, respectively. Assuming that the magnitudes of acceleration and deceleration are the same, find (a) the true weight of the person and (b) the magnitude of the acceleration. Take g = 9.9 m/s2.
Consider the Atwood machine of the previous problem. The larger mass is stopped for a moment, 2.0 s after the system is set into motion. Find the time that elapses before the string is tight again.
Let m1 = 1 kg, m2 = 2 kg and m3 = 3 kg in the following figure. Find the accelerations of m1, m2 and m3. The string from the upper pulley to m1 is 20 cm when the system is released from rest. How long will it take before m1 strikes the pulley?
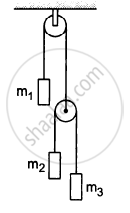
In the previous problem, suppose m2 = 2.0 kg and m3 = 3.0 kg. What should be the mass m, so that it remains at rest?
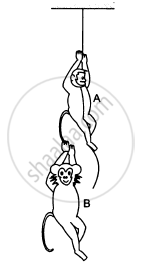
The monkey B, shown in the following figure, is holding on to the tail of monkey A that is climbing up a rope. The masses of monkeys A and B are 5 kg and 2 kg, respectively. If A can tolerate a tension of 30 N in its tail, what force should it apply on the rope in order to carry monkey B with it? Take g = 10 m/s2.
A block is kept on the floor of an elevator at rest. The elevator starts descending with an acceleration of 12 m/s2. Find the displacement of the block during the first 0.2 s after the start. Take g = 10 m/s2.
Two balls A and B of masses m and 2 m are in motion with velocities 2v and v, respectively. Compare:
(i) Their inertia.
(ii) Their momentum.
(iii) The force needed to stop them in the same time.
Calculate the magnitude of force which when applied on a body of mass 0.5 kg produces an acceleration of 5 m s-2.
A bullet of mass 50 g moving with an initial velocity 100 m s-1 strikes a wooden block and comes to rest after penetrating a distance 2 cm in it. Calculate: (i) Initial momentum of the bullet, (ii) Final momentum of the bullet, (iii) Retardation caused by the wooden block and (iv) Resistive force exerted by the wooden block.
A stone is dropped freely from the top of a tower and it reaches the ground in 4 s. Taking g = 10m s-2, calculate the height of the tower.
Prove mathematically F = ma
Name the physical quantity which equals the rate of change of linear momentum.
A cricket ball of mass 150 g has an initial velocity `u = (3hati + 4hatj)` m s−1 and a final velocity `v = - (3hati + 4hatj)` m s−1 after being hit. The change in momentum (final momentum-initial momentum) is (in kg m s1)
The motion of a particle of mass m is given by x = 0 for t < 0 s, x(t) = A sin 4 pt for 0 < t < (1/4) s (A > o), and x = 0 for t > (1/4) s. Which of the following statements is true?
- The force at t = (1/8) s on the particle is – 16π2 Am.
- The particle is acted upon by on impulse of magnitude 4π2 A m at t = 0 s and t = (1/4) s.
- The particle is not acted upon by any force.
- The particle is not acted upon by a constant force.
- There is no impulse acting on the particle.
A woman throws an object of mass 500 g with a speed of 25 ms1.
- What is the impulse imparted to the object?
- If the object hits a wall and rebounds with half the original speed, what is the change in momentum of the object?
