Advertisements
Advertisements
प्रश्न
A man running a racecourse notes that the sum of the distances from the two flag posts form him is always 10 m and the distance between the flag posts is 8 m. find the equation of the posts traced by the man.
उत्तर
Let F1 and F2 be two points where the flag posts are fixed on the ground.
The origin O is the mid-point of F1F2.
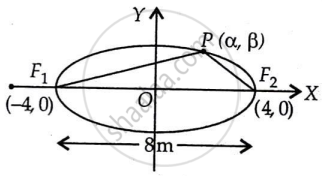
∴ OF1 - OF2 = `1/2 F_1F_2 = 1/2 xx 8 = 4m`
Coordinates of F1 are (-4, 0) and F2 are (4, 0)
Let P (α, β) be any point on the track.
∴ PF1 + PF2 = 10
∴ `sqrt((α + 4)^2 + (β - 0)^2)` + `sqrt((α - 4)^2 + (β - 0)^2) = 10`
= `sqrt(α^2 + 16 + 8α + β^2)` = `10 - sqrt(α^2 + 16 - 8α + β^2)`
Squaring both sides, we get
α2 + β2 + 8α + 16 = 100 + α2 + β2 - Bα + 16 `-20 sqrt(α^2 + β^2 - 8α + 16)`
= 16α - 100 = `-20 sqrt(α^2 + β^2 - 8α + 16)`
Again, squaring both sides, we get
= (16α - 100)2 = (`-20 sqrt((α^2 + β^2 - 8α + 16)^2)`
= 256α2 + 10000 - 3200α = 400(α2 + β2 - 8α+ 16)
= 256α2 + 10000 - 3200α = 400α2 + 400β2 - 32008α+ 6400)
= 144α2 + 400β2 = 3600
= `(144α^2)/(3600) + (400β^2)/(3600) = 1`
Thus, the required equation of locus of point P is `x^2/25 + y^2/9 = 1`.
APPEARS IN
संबंधित प्रश्न
Find the equation for the ellipse that satisfies the given condition:
Vertices (±5, 0), foci (±4, 0)
Find the equation for the ellipse that satisfies the given conditions:
Vertices (±6, 0), foci (±4, 0)
Find the equation for the ellipse that satisfies the given conditions:
Ends of major axis (0, `+- sqrt5`), ends of minor axis (±1, 0)
Find the equation for the ellipse that satisfies the given conditions:
Length of major axis 26, foci (±5, 0)
Find the equation for the ellipse that satisfies the given conditions:
Length of minor axis 16, foci (0, ±6)
Find the equation for the ellipse that satisfies the given conditions:
b = 3, c = 4, centre at the origin; foci on the x axis.
Find the equation for the ellipse that satisfies the given conditions:
Centre at (0, 0), major axis on the y-axis and passes through the points (3, 2) and (1, 6)
Find the equation of the ellipse in the case:
focus is (0, 1), directrix is x + y = 0 and e = \[\frac{1}{2}\] .
Find the equation of the ellipse in the case:
focus is (−2, 3), directrix is 2x + 3y + 4 = 0 and e = \[\frac{4}{5}\]
Find the equation of the ellipse in the case:
focus is (1, 2), directrix is 3x + 4y − 5 = 0 and e = \[\frac{1}{2}\]
Find the equation to the ellipse (referred to its axes as the axes of x and y respectively) which passes through the point (−3, 1) and has eccentricity \[\sqrt{\frac{2}{5}}\]
Find the equation of the ellipse in the case:
eccentricity e = \[\frac{1}{2}\] and foci (± 2, 0)
Find the equation of the ellipse in the case:
eccentricity e = \[\frac{1}{2}\] and semi-major axis = 4
Find the equation of the ellipse in the case:
eccentricity e = \[\frac{1}{2}\] and major axis = 12
Find the equation of the ellipse in the case:
The ellipse passes through (1, 4) and (−6, 1).
Find the equation of the ellipse in the case:
Vertices (± 5, 0), foci (± 4, 0)
Find the equation of the ellipse in the case:
Vertices (0, ± 13), foci (0, ± 5)
Find the equation of the ellipse in the following case:
Vertices (± 6, 0), foci (± 4, 0)
Find the equation of the ellipse in the following case:
Ends of major axis (± 3, 0), ends of minor axis (0, ± 2)
Find the equation of the ellipse in the following case:
Ends of major axis (0, ±\[\sqrt{5}\] ends of minor axis (± 1, 0)
Find the equation of the ellipse in the following case:
Length of major axis 26, foci (± 5, 0)
Find the equation of the ellipse in the following case:
Length of minor axis 16 foci (0, ± 6)
Find the equation of the ellipse in the following case:
Foci (± 3, 0), a = 4
A bar of given length moves with its extremities on two fixed straight lines at right angles. Any point of the bar describes an ellipse.
The line 2x + 3y = 12 touches the ellipse `x^2/9 + y^2/4` = 2 at the point (3, 2).
An ellipse is described by using an endless string which is passed over two pins. If the axes are 6 cm and 4 cm, the length of the string and distance between the pins are ______.
