Advertisements
Advertisements
प्रश्न
A metre long narrow bore held horizontally (and closed at one end) contains a 76 cm long mercury thread, which traps a 15 cm column of air. What happens if the tube is held vertically with the open end at the bottom?
उत्तर १
When the tube is held horizontally, the mercury thread of length 76 cm traps a length of air = 15 cm. A length of 9 cm of the tube will be left at the open end. The pressure of air enclosed in tube will be atmospheric pressure. Let area of cross-section of the tube be 1 sq. cm.
.’. P1 = 76 cm and V1 = 15 cm3
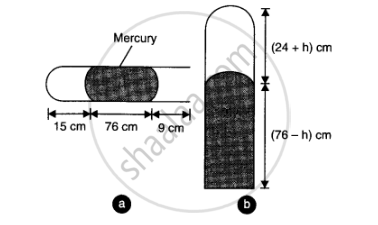
When the tube is held vertically, 15 cm air gets another 9 cm of air (filled in the right handside in the horizontal position) and let h cm of mercury flows out to balance the atmospheric pressure. Then the heights of air column and mercury column are (24 + h) cm and (76 – h) cm respectively.
The pressure of air = 76 - (76 - h) = h cm of mercury
`:. V_2 = (24 + h) cm^3` and `P_2 = h cm`
if we assume that temperature remain constant then
`P_1V_1 = P_2V_2 or 76 xx 15 = h xx (24 + h ) or h^2 + 24h - 1140 = 0`
or `h = (-24 +- sqrt((24)^2 + 4xx 1140))/2` = 23.8 cm or - 47.8 cm
Since h cannot be negative (because more mercury cannot flow into tube), there fore h = 23.8 cm
Thus in the verticle position of the tube , 23.8 cm of mercury flow out
उत्तर २
Length of the narrow bore, L = 1 m = 100 cm
Length of the mercury thread, l = 76 cm
Length of the air column between mercury and the closed end, la = 15 cm
Since the bore is held vertically in air with the open end at the bottom, the mercury length that occupies the air space is: 100 – (76 + 15) = 9 cm
Hence, the total length of the air column = 15 + 9 = 24 cm
Let h cm of mercury flow out as a result of atmospheric pressure.
∴Length of the air column in the bore = 24 + h cm
And, length of the mercury column = 76 – h cm
Initial pressure, P1 = 76 cm of mercury
Initial volume, V1 = 15 cm3
Final pressure, P2 = 76 – (76 – h) = h cm of mercury
Final volume, V2 = (24 + h) cm3
Temperature remains constant throughout the process.
∴P1V1 = P2V2
76 × 15 = h (24 + h)
h2 + 24h – 1140 = 0
`:. h = (-24+-sqrt((24)^2 + 4xx 1xx 1140))/(2xx1)`
= 23.8 cm or –47.8 cm
Height cannot be negative. Hence, 23.8 cm of mercury will flow out from the bore and 52.2 cm of mercury will remain in it. The length of the air column will be 24 + 23.8 = 47.8 cm.
APPEARS IN
संबंधित प्रश्न
Does a solid also have two kinds of molar heat capacities Cp and Cv? If yes, is Cp > Cv? Or is Cp − Cv = R?
In a real gas, the internal energy depends on temperature and also on volume. The energy increases when the gas expands isothermally. Examining the derivation of Cp − Cv = R, find whether Cp − Cv will be more than R, less than R or equal to R for a real gas.
Show that the slope of the p−V diagram is greater for an adiabatic process compared to an isothermal process.
Can two states of an ideal gas be connected by an isothermal process as well as an adiabatic process?
5 g of a gas is contained in a rigid container and is heated from 15°C to 25°C. Specific heat capacity of the gas at constant volume is 0.172 cal g−1 °C−1 and the mechanical equivalent of heat is 4.2 J cal−1. Calculate the change in the internal energy of the gas
A sample of air weighing 1.18 g occupies 1.0 × 103 cm3 when kept at 300 K and 1.0 × 105 Pa. When 2.0 cal of heat is added to it at constant volume, its temperature increases by 1°C. Calculate the amount of heat needed to increase the temperature of air by 1°C at constant pressure if the mechanical equivalent of heat is 4.2 × 107 erg cal−1. Assume that air behaves as an ideal gas.
An ideal gas expands from 100 cm3 to 200 cm3 at a constant pressure of 2.0 × 105 Pa when 50 J of heat is supplied to it. Calculate (a) the change in internal energy of the gas (b) the number of moles in the gas if the initial temperature is 300 K (c) the molar heat capacity Cp at constant pressure and (d) the molar heat capacity Cv at constant volume.
In Joly's differential steam calorimeter, 3 g of an ideal gas is contained in a rigid closed sphere at 20°C. The sphere is heated by steam at 100°C and it is found that an extra 0.095 g of steam has condensed into water as the temperature of the gas becomes constant. Calculate the specific heat capacity of the gas in J g−1 K−1. The latent heat of vaporisation of water = 540 cal g−1
Air (γ = 1.4) is pumped at 2 atm pressure in a motor tyre at 20°C. If the tyre suddenly bursts, what would be the temperature of the air coming out of the tyre? Neglect any mixing with the atmospheric air.
The figure shows two vessels with adiabatic walls, one containing 0.1 g of helium (γ = 1.67, M = 4 g mol−1) and the other containing some amount of hydrogen (γ = 1.4, M = 2 g mol−1). Initially, the temperatures of the two gases are equal. The gases are electrically heated for some time during which equal amounts of heat are given to the two gases. It is found that the temperatures rise through the same amount in the two vessels. Calculate the mass of hydrogen.