Advertisements
Advertisements
प्रश्न
A particle is performing S.H.M. of amplitude 5 cm and period of 2s. Find the speed of the particle at a point where its acceleration is half of its maximum value.
उत्तर
Given:
A = 5 cm = 5 × 10−2 m, T = 2 s,
a = `"a"_"max"/2 = ("Aomega^2)/2` ….(i)
To find: speed (v)
Formula: v = `omegasqrt("A"^2 - "x"^2)`
Calculation:
Since, a = ω2x
∴ x = `"a"/ω^2 = ("A"ω^2)/(2ω^2) = "A"/2` ….[from (i)]
From formula,
v = `ωsqrt("A"^2 - "A"^2/4) = sqrt3/2"A"ω`
= `sqrt3/2 xx 5 xx 10^-2 xx (2pi)/"T"` .....`[∵ ω = (2pi)/"T"]`
= `sqrt3/2 xx 5 xx 10^-2 xx (2 xx 3.14)/2`
∴ v = 13.6 × 10−2 m/s
The speed of the particle where its acceleration is half of its maximum value is 13.6 × 10−2 m/s.
APPEARS IN
संबंधित प्रश्न
Choose the correct option:
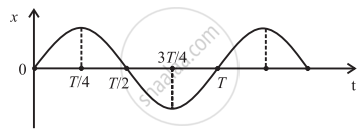
The graph shows variation of displacement of a particle performing S.H.M. with time t. Which of the following statements is correct from the graph?
A particle is performing simple harmonic motion with amplitude A and angular velocity ω. The ratio of maximum velocity to maximum acceleration is ______.
For a particle performing SHM when displacement is x, the potential energy and restoring force acting on it is denoted by E and F, respectively. The relation between x, E and F is ____________.
Two identical wires of substances 'P' and 'Q ' are subjected to equal stretching force along the length. If the elongation of 'Q' is more than that of 'P', then ______.
A wheel of M.I. 50 kg m2 starts rotating on applying a constant torque of 200 Nm. Its angular velocity after 2.5 second from the start is ______.
A particle is moving along a circular path of radius 6 m with a uniform speed of 8 m/s. The average acceleration when the particle completes one-half of the revolution is ______.
A body performing a simple harmonic motion has potential energy 'P1' at displacement 'x1' Its potential energy is 'P2' at displacement 'x2'. The potential energy 'P' at displacement (x1 + x2) is ________.
If 'α' and 'β' are the maximum velocity and maximum acceleration respectively, of a particle performing linear simple harmonic motion, then the path length of the particle is _______.
The distance covered by a particle undergoing SHM in one time period is (amplitude = A) ____________.
Which of the following represents the acceleration versus displacement graph of SHM?
The length of the second's pendulum is decreased by 0.3 cm when it is shifted from place A to place B. If the acceleration due to gravity at place A is 981 cm/s2, the acceleration due to gravity at place B is ______ (Take π2 = 10)
A body is executing S.H.M. Its potential energy is E1 and E2 at displacements x and y respectively. The potential energy at displacement (x + y) is ______.
A simple pendulum of length 'L' is suspended from a roof of a trolley. A trolley moves in horizontal direction with an acceleration 'a'. What would be the period of oscillation of a simple pendulum?
(g is acceleration due to gravity)
A block of mass 16 kg moving with velocity 4 m/s on a frictionless surface compresses an ideal spring and comes to rest. If force constant of the spring is 100 N/m then how much will be the spring compressed?
The displacement of the particle performing S.H.M. is given by x = 4 sin πt, where x is in cm and t is in second. The time taken by the particle in second to move from the equilibrium position to the position of half the maximum displacement, is ______.
`[sin30^circ=cos60^circ=0.5, cos30^circ=sin60^circ=sqrt3/2]`
The displacement of a particle in S.H.M. is x = A cos `(omegat+pi/6).` Its speed will be maximum at time ______.
The displacements of two particles executing simple harmonic motion are represented as y1 = 2 sin (10t + θ) and y2 = 3 cos 10t. The phase difference between the velocities of these waves is ______.
A body perform linear simple harmonic motion of amplitude 'A'. At what displacement from the mean position, the potential energy of the body is one fourth of its total energy?
A particle performs linear SHM at a particular instant, velocity of the particle is 'u' and acceleration is a while at another instant velocity is 'v' and acceleration is 'β (0 < α < β). The distance between the two position is ______.
In figure, a particle is placed at the highest point A of a smooth sphere of radius r. It is given slight push and it leaves the sphere at B, at a depth h vertically below A, such that h is equal to ______.

