Advertisements
Advertisements
प्रश्न
A particle is performing simple harmonic motion with amplitude A and angular velocity ω. The ratio of maximum velocity to maximum acceleration is ______.
पर्याय
ω
1/ω
ω2
A/ω
उत्तर
A particle is performing simple harmonic motion with amplitude A and angular velocity ω. The ratio of maximum velocity to maximum acceleration is 1/ω.
APPEARS IN
संबंधित प्रश्न
Choose the correct option:
The graph shows variation of displacement of a particle performing S.H.M. with time t. Which of the following statements is correct from the graph?
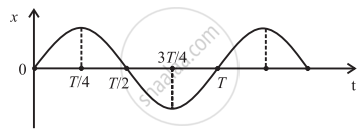
Answer in brief.
Using differential equations of linear S.H.M, obtain the expression for (a) velocity in S.H.M., (b) acceleration in S.H.M.
Find the change in length of a second’s pendulum, if the acceleration due to gravity at the place changes from 9.75 m/s2 to 9.8 m/s2.
The light of wavelength '`lambda`'. incident on the surface of metal having work function `phi` emits the electrons. The maximum velocity of electrons emitted is ______.
[c = velocity of light, h = Planck's constant, m = mass of electron]
For a particle performing SHM when displacement is x, the potential energy and restoring force acting on it is denoted by E and F, respectively. The relation between x, E and F is ____________.
A wheel of M.I. 50 kg m2 starts rotating on applying a constant torque of 200 Nm. Its angular velocity after 2.5 second from the start is ______.
A particle is moving along a circular path of radius 6 m with a uniform speed of 8 m/s. The average acceleration when the particle completes one-half of the revolution is ______.
The relation between time and displacement for two particles is given by Y1 = 0.06 sin 27`pi` (0.04t + `phi_1`), y2 = 0.03sin 27`pi`(0.04t + `phi_2`). The ratio of the intensity of the waves produced by the vibrations of the two particles will be ______.
If 'α' and 'β' are the maximum velocity and maximum acceleration respectively, of a particle performing linear simple harmonic motion, then the path length of the particle is _______.
A particle executing S.H.M. has amplitude 0.01 m and frequency 60 Hz. The maximum acceleration of the particle is ____________.
The maximum speed of a particle in S.H.M. is 'V'. The average speed is ______
A body is executing S.H.M. Its potential energy is E1 and E2 at displacements x and y respectively. The potential energy at displacement (x + y) is ______.
A simple pendulum of length 'L' is suspended from a roof of a trolley. A trolley moves in horizontal direction with an acceleration 'a'. What would be the period of oscillation of a simple pendulum?
(g is acceleration due to gravity)
The bob of a simple pendulum is released at time t = 0 from a position of small angular displacement. Its linear displacement is ______.
(l = length of simple pendulum and g = acceleration due to gravity, A = amplitude of S.H.M.)
The displacement of the particle performing S.H.M. is given by x = 4 sin πt, where x is in cm and t is in second. The time taken by the particle in second to move from the equilibrium position to the position of half the maximum displacement, is ______.
`[sin30^circ=cos60^circ=0.5, cos30^circ=sin60^circ=sqrt3/2]`
The displacement of a particle in S.H.M. is x = A cos `(omegat+pi/6).` Its speed will be maximum at time ______.
A body perform linear simple harmonic motion of amplitude 'A'. At what displacement from the mean position, the potential energy of the body is one fourth of its total energy?
A particle performs linear SHM at a particular instant, velocity of the particle is 'u' and acceleration is a while at another instant velocity is 'v' and acceleration is 'β (0 < α < β). The distance between the two position is ______.
In figure, a particle is placed at the highest point A of a smooth sphere of radius r. It is given slight push and it leaves the sphere at B, at a depth h vertically below A, such that h is equal to ______.

A spring of force constant of 400 N/m is loaded with a mass of 0.25 kg. The amplitude of oscillations is 4 cm. When mass comes to the equilibrium position. Its velocity is ______.
The displacement of a particle of mass 3 g executing simple harmonic motion is given by Y = 3 sin (0.2 t) in SI units. The kinetic energy of the particle at a point which is at a distance equal to `1/3` of its amplitude from its mean position is ______.
Which one of the following is not a characteristics of SHM?
