Advertisements
Advertisements
प्रश्न
Find the change in length of a second’s pendulum, if the acceleration due to gravity at the place changes from 9.75 m/s2 to 9.8 m/s2.
उत्तर
Data: gf =9.75 m/s2 , g2 = 9.8 m/s2
Length of a seconds pendulum, L = `"g"/π^2`
∴ L1 = `"g"_1/"π"^2=9.75/9.872` = 0.9876 m
and L2 = `"g"_2/π^2=9.8/9.872` = 0.9927 m
Find the change in length
ΔL = L2 − L1
= 0.9927 − 0.9876
= 0.0051 m = 5.1 mm
∴ The length of the second's pendulum must be increased from 0.9876 m to 0.9927 m, i.e., by 0.0051 m.
APPEARS IN
संबंधित प्रश्न
Choose the correct option:
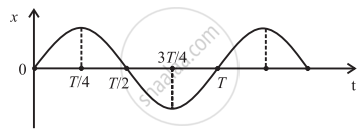
The graph shows variation of displacement of a particle performing S.H.M. with time t. Which of the following statements is correct from the graph?
A particle is performing simple harmonic motion with amplitude A and angular velocity ω. The ratio of maximum velocity to maximum acceleration is ______.
Acceleration of a particle executing S.H.M. at its mean position.
A particle is performing S.H.M. of amplitude 5 cm and period of 2s. Find the speed of the particle at a point where its acceleration is half of its maximum value.
For a particle performing SHM when displacement is x, the potential energy and restoring force acting on it is denoted by E and F, respectively. The relation between x, E and F is ____________.
Two identical wires of substances 'P' and 'Q ' are subjected to equal stretching force along the length. If the elongation of 'Q' is more than that of 'P', then ______.
The displacement of a particle from its mean position (in metre) is given by, y = 0.2 sin(10 πt + 1.5π) cos(10 πt + 1.5π).
The motion of particle is ____________.
In U.C.M., when time interval δt → 0, the angle between change in velocity (δv) and linear velocity (v) will be ______.
A wheel of M.I. 50 kg m2 starts rotating on applying a constant torque of 200 Nm. Its angular velocity after 2.5 second from the start is ______.
If 'α' and 'β' are the maximum velocity and maximum acceleration respectively, of a particle performing linear simple harmonic motion, then the path length of the particle is _______.
A particle executing S.H.M. has amplitude 0.01 m and frequency 60 Hz. The maximum acceleration of the particle is ____________.
The displacement of a particle is 'y' = 2 sin `[(pit)/2 + phi]`, where 'y' is cm and 't' in second. What is the maximum acceleration of the particle executing simple harmonic motion?
(Φ = phase difference)
The length of the second's pendulum is decreased by 0.3 cm when it is shifted from place A to place B. If the acceleration due to gravity at place A is 981 cm/s2, the acceleration due to gravity at place B is ______ (Take π2 = 10)
A body is executing S.H.M. Its potential energy is E1 and E2 at displacements x and y respectively. The potential energy at displacement (x + y) is ______.
A block of mass 16 kg moving with velocity 4 m/s on a frictionless surface compresses an ideal spring and comes to rest. If force constant of the spring is 100 N/m then how much will be the spring compressed?
In figure, a particle is placed at the highest point A of a smooth sphere of radius r. It is given slight push and it leaves the sphere at B, at a depth h vertically below A, such that h is equal to ______.

A spring of force constant of 400 N/m is loaded with a mass of 0.25 kg. The amplitude of oscillations is 4 cm. When mass comes to the equilibrium position. Its velocity is ______.
A body of mass 0.5 kg travels in a straight line with velocity v = ax3/2 where a = 5 m–1/2s–1. The change in kinetic energy during its displacement from x = 0 to x = 2 m is ______.
Calculate the velocity of a particle performing S.H.M. after 1 second, if its displacement is given by x = `5sin((pit)/3)`m.
State the expressions for the displacement, velocity and acceleration draw performing linear SHM, starting from the positive extreme position. Hence, their graphs with respect to time.
State the expression for the total energy of SHM in terms of acceleration.
Which one of the following is not a characteristics of SHM?
A particle executing SHM has velocities v1 and v2 when it is at distance x1 and x2 from the centre of the path. Show that the time period is given by `T=2pisqrt((x_2^2-x_1^2)/(v_1^2-v_2^2))`
