Advertisements
Advertisements
प्रश्न
A point P (–2, 3) is reflected in line x = 2 to point P’. Find the co-ordinates of P’.
उत्तर
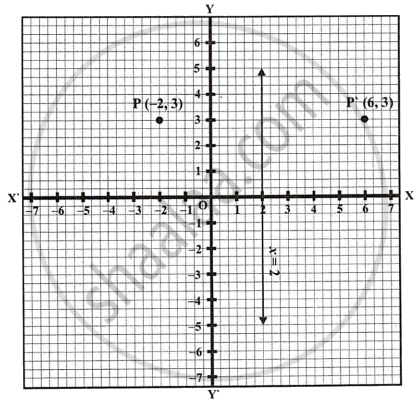
The image of P (–2, 3) is P' which is reflected in the line x = 2.
The co-ordinates of P' will be (6, 3) as shown in the graph.
APPEARS IN
संबंधित प्रश्न
Attempt this question on graph paper.
- Plot A (3, 2) and B (5, 4) on graph paper. Take 2 cm = 1 unit on both the axes.
- Reflect A and B in the x-axis to A’ and B’ respectively. Plot these points also on the same graph paper.
- Write down:
- the geometrical name of the figure ABB’A’;
- the measure of angle ABB’;
- the image of A” of A, when A is reflected in the origin.
- the single transformation that maps A’ to A”.
Points (3, 0) and (–1, 0) are invariant points under reflection in the line L1; points (0, –3) and (0, 1) are invariant points on reflection in line L2.
- Name or write equations for the lines L1 and L2.
- Write down the images of the points P (3, 4) and Q (–5, –2) on reflection in line L1. Name the images as P’ and Q’ respectively.
- Write down the images of P and Q on reflection in L2. Name the images as P” and Q” respectively.
- State or describe a single transformation that maps P’ onto P''.
- Point P (a, b) is reflected in the x-axis to P’ (5, –2). Write down the values of a and b.
- P” is the image of P when reflected in the y-axis. Write down the co-ordinates of P”.
- Name a single transformation that maps P’ to P”.
The points P (4, 1) and Q (–2, 4) are reflected in line y = 3. Find the co-ordinates of P’, the image of P and Q’, the image of Q.
Points A and B have co-ordinates (3, 4) and (0, 2) respectively. Find the image:
- A’ of A under reflection in the x-axis.
- B’ of B under reflection in the line AA’.
- A” of A under reflection in the y-axis.
- B” of B under reflection in the line AA”.
The point P (5, 3) was reflected in the origin to get the image P’.
- Write down the co-ordinates of P’.
- If M is the foot of the perpendicular from P to the x-axis, find the co-ordinates of M.
- If N is the foot of the perpendicular from P’ to the x-axis, find the co-ordinates of N.
- Name the figure PMP’N.
- Find the area of the figure PMP’N.
The point P (3, 4) is reflected to P’ in the x-axis; and O’ is the image of O (the origin) when reflected in the line PP’. Write:
- the co-ordinates of P’ and O’.
- the length of the segments PP’ and OO’.
- the perimeter of the quadrilateral POP’O’.
- the geometrical name of the figure POP’O’.
The triangle ABC, where A is (2, 6), B is (–3, 5) and C is (4, 7), is reflected in the y-axis to triangle A'B'C'. Triangle A'B'C' is then reflected in the origin to triangle A"B"C".
- Write down the co-ordinates of A", B" and C".
- Write down a single transformation that maps triangle ABC onto triangle A"B"C".
Using a graph paper, plot the point A (6, 4) and B (0, 4).
(a) Reflect A and B in the origin to get the image A’ and B’.
(b) Write the co-ordinates of A’ and B’.
(c) Sate the geometrical name for the figure ABA’B’.
(d) Find its perimeter.
Use graph paper for this question.
(Take 2 cm = 1 unit along both x-axis and y-axis.)
Plot the points O(0, 0), A(–4, 4), B(–3, 0) and C(0, –3).
- Reflect points A and B on the y-axis and name them A' and B' respectively. Write down their co-ordinates.
- Name the figure OABCB'A'.
- State the line of symmetry of this figure.
