Advertisements
Advertisements
рдкреНрд░рд╢реНрди
A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 13 cm, 14 cm and 15 cm and the parallelogram stands on the base 14 cm, find the height of the parallelogram.
Advertisements
рдЙрддреНрддрд░
The sides of a triangle DCE are
DC = 15 cm, CE = 13 cm, ED = 14 cm
Let h be the height of parallelogram ABCD
Given,
Perimeter of ΔDCE
2s = DC + CE + ED
`⇒S=1/2(15+13+4)`
`⇒s=1/2(42)`
`⇒s=21cm`
ЁЭР┤ЁЭСЯЁЭСТЁЭСО ЁЭСЬЁЭСУ ΔЁЭР╖ЁЭР╢ЁЭР╕ = `sqrt(s(s-dc)(s-ce)(s-ed))`
`=sqrt(21(21-15)(21-13)(21-14))`
`=sqrt(21xx7xx8xx6)`
`=sqrt(84xx84)`
`84 cm^2`
Given that
Area of ΔЁЭСЩЁЭСТ ЁЭР╖ЁЭР╢ЁЭР╕= ЁЭСОЁЭСЯЁЭСТЁЭСО ЁЭСЬЁЭСУ ЁЭР┤ЁЭР╡ЁЭР╢ЁЭР╖
= Area of parallelogram ABCD = =`84cm^2`
⇒ 24×тДО=84 [∴ Area of parallelogram = base × height]
⇒ h = 6 cm
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНтАНрди
The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122m, 22m, and 120m (see the given figure). The advertisements yield an earning of тВ╣ 5000 per m2 per year. A company hired one of its walls for 3 months. How much rent did it pay?
The perimeter of a triangular field is 240 dm. If two of its sides are 78 dm and 50 dm, find the length of the perpendicular on the side of length 50 dm from the opposite vertex.
The perimeter of an isosceles triangle is 42 cm and its baše is (32) times each of the equal sides. Find the length of each side of the triangle, area of the triangle and the height of the triangle.
The adjacent sides of a parallelogram ABCD measure 34 cm and 20 cm, and the diagonal AC measures 42 cm. Find the area of the parallelogram.
Determine whether the sets of points are collinear?
`(-1/2, 3), (-5, 6) and (-8, 8)`
Find the area of triangle FED
Find the area of a triangle formed by the lines 3x + y – 2 = 0, 5x + 2y – 3 = 0 and 2x – y – 3 = 0
The perimeter of an isosceles triangle is 32 cm. The ratio of the equal side to its base is 3 : 2. Find the area of the triangle.
Find the area of a parallelogram given in figure. Also find the length of the altitude from vertex A on the side DC.
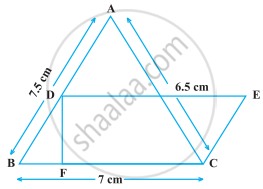
In the following figure, тИЖABC has sides AB = 7.5 cm, AC = 6.5 cm and BC = 7 cm. On base BC a parallelogram DBCE of same area as that of тИЖABC is constructed. Find the height DF of the parallelogram.
