Advertisements
Advertisements
प्रश्न
एका आयताचे क्षेत्रफळ 192 चौसेमी असून त्याची लांबी 16 सेमी आहे, तर त्या आयताच्या कर्णाची लांबी माहीत करण्यासाठी कृती पूर्ण करा.
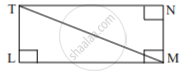
कृती: सोबतच्या आकृतीत, `square`LMNT हा आयत आहे.
आयताचे क्षेत्रफळ = लांबी × रुंदी
∴ आयताचे क्षेत्रफळ = `square` × रुंदी
रुंदी = 12 सेमी
∠TLM = 90° [आयताचा प्रत्येक कोन काटकोन असतो.]
∆TLM मध्ये, पायथागोरसच्या प्रमेयानुसार,
TL2 + `square` = TM2
TM2 = `square` + 122
TM2 = `square` + 144
TM = 20
उत्तर
सोबतच्या आकृतीत, `square`LMNT हा आयत आहे.
आयताचे क्षेत्रफळ = लांबी × रुंदी
∴ आयताचे क्षेत्रफळ = 16 × रुंदी
∴ 192 = 16 × रुंदी
∴ रुंदी = `192/16`
∴ रुंदी = 12 सेमी
∴ ΤL = 12 सेमी, LM = 16 सेमी …(i)
∠TLM = 90° [आयताचा प्रत्येक कोन काटकोन असतो.]
∆TLM मध्ये, पायथागोरसच्या प्रमेयानुसार,
TL2 + LM2 = TM2
TM2 = `underline(16^2)` + 122 ..............(i) वरून
TM2 = 256 + 144
TM2 = 400
TM = 20
APPEARS IN
संबंधित प्रश्न
एका चौरसाचा कर्ण 10 सेमी आहे तर त्याच्या बाजूची लांबी व परिमिती काढा.
रस्त्याच्या दुतर्फा असलेल्या इमारतीच्या भिंती एकमेकींना समांतर आहेत. 5.8 मी लांबीच्या शिडीचे एक टोक रस्त्यावर ठेवले असता तिचे वरचे टोक पहिल्या इमारतीच्या 4 मीटर उंच असलेल्या खिडकीपर्यंत टेकते. त्याच ठिकाणी शिडी ठेवून रस्त्याच्या दुसऱ्या बाजूस वळविल्यास तिचे वरचे टोक दुसऱ्या इमारतीच्या 4.2 मीटर उंच असलेल्या खिडकीपर्यंत येते, तर रस्त्याची रुंदी काढा.
बाजूंच्या लांबी a, b, c असलेल्या त्रिकोणामध्ये जर a2 + b2 = c2 असेल तर तो कोणत्या प्रकारचा त्रिकोण असेल?
काटकोन त्रिकोणामध्ये काटकोन करणाऱ्या बाजू 24 सेमी व 18 सेमी असतील तर त्याच्या कर्णाची लांबी ______ असेल.
समद्विभुज काटकोन त्रिकोणाची बाजू x आहे, तर त्याच्या कर्णाची लांबी काढा.
आयताचे क्षेत्रफळ 192 चौसेमी असून त्याची लांबी 16 सेमी आहे, तर आयताच्या कर्णाची लांबी काढा.
पुढील प्रत्येक उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक उत्तराचा योग्य पर्याय निवडून त्याचे वर्णाक्षर लिहा.
एका समभुज चौकोनाच्या कर्णाची लांबी अनुक्रमे 60 व 80 असेल, तर त्या समभुज चौकोनाच्या बाजूची लांबी किती?
सोबतच्या आकृतीत, ∆ABC मध्ये, AD ⊥ BC, तर AB2 + CD2 = BD2 + AC2 हे सिद्ध करण्यासाठी खालील कृती पूर्ण करा.
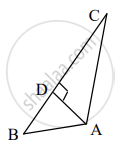
कृती: पायथागोरसच्या प्रमेयानुसार, काटकोन त्रिकोण ∆ADC मध्ये,
AC2 = AD2 + `square^2`
∴ AD2 = AC2 – CD2 …...........(i)
तसेच, पायथागोरसच्या प्रमेयानुसार, काटकोन त्रिकोण ∆ABD मध्ये,
AB2 = `square^2` + BD2
∴ AD2 = AB2 – BD2 …...… (ii)
∴ `square^2 - "BD"^2 = "AC"^2 - square^2` .....…….. (i) व (ii) वरून
∴ AB2 + CD2 = AC2 + BD2
समद्विभुज काटकोन त्रिकोणाच्या एकरूप बाजूंची लांबी 7 सेमी आहे. त्याची परिमिती काढा.
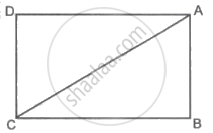
वरील आकृतीत `square`ABCD हा आयत आहे. जर AB = 5, AC = 13, तर बाजू BC ची लांबी काढण्यासाठी खालील कृती पर्ण करा.
कृती: ΔABC हा `square` त्रिकोण आहे.
∴ पायथागोरसच्या प्रमेयानुसार,
AB2 + BC2 = AC2
∴ 25 + BC2 = `square`
∴ BC2 = `square`
∴ BC = `square`
