Advertisements
Advertisements
प्रश्न
ABCD is a parallelogram in which ∠A = 70°. Compute ∠B, ∠C and ∠D .
उत्तर
In a parallelogram ABCD.
`∠`A = 70°
`∠`A = `∠`B = 180° [ ∴ Adjacent angles supplementary]
70° + `∠`B = 180° `∠`A = 70°]
`∠`B =180° - 70°
=110°
In a parallelogram opposite sides are equal
`∠`A = `∠`C = 70°
`∠`B = `∠`D = 110°
APPEARS IN
संबंधित प्रश्न
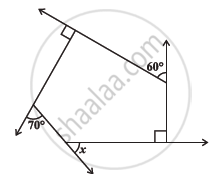
Find the angle measure x in the given Figure
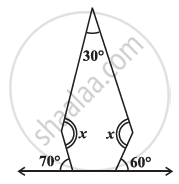
Find the angle measure x in the given Figure
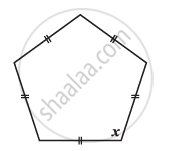
Find x in the following figures.
Three angles of a quadrilateral are respectively equal to 110°, 50° and 40°. Find its fourth angle
In a quadrilateral ABCD, CO and DO are the bisectors of `∠`C and ∠D respectively. Prove that
`∠`COD = `1/2` (`∠`A+ `∠`B).
PQRS is a square such that PR and SQ intersect at O. State the measure of ∠POQ.
In ΔABC, ∠A = 30°, ∠B = 40° and ∠C = 110°. The angles of the triangle formed by joining the mid-points of the sides of this triangle are
Can all the angles of a quadrilateral be right angles? Give reason for your answer.
One angle of a quadrilateral is of 108º and the remaining three angles are equal. Find each of the three equal angles.
In the following figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. Prove that AD = 2CD.

