Question

An aeroplane is flying along the line `vecr = λ(hati - hatj + hatk)`; where 'λ' is a scalar and another aeroplane is flying along the line `vecr = hati - hatj + μ(-2hatj + hatk)`; where 'μ' is a scalar. At what points on the lines should they reach, so that the distance between them is the shortest? Find the shortest possible distance between them.

Answer 1

Given that equation of lines are 

`vecr = λ(hati - hatj + hatk)`    ...(i)

and `vecr = hati - hatj + μ(-2hatj + hatk)`   ...(ii)

The given lines are non-parallel lines as vectors `hati - hatj + hatk` and `-2hatj + hatk` are not parallel. There is a unique line segment PQ (P lying on line (i) and Q on the other line (ii)), which is at right angles to both the lines. PQ is the shortest distance between the lines. Hence, the shortest possible distance between the aeroplanes = PQ.

Let the position vector of the point P lying on the line `vecr = λ(hati - hatj + hatk)` where 'λ' is a scalar, is

`λ(hati - hatj + hatk)`, for some λ and the position vector of the point Q lying on the line

`vecr = hati - hatj + μ(-2hatj + hatk)`; where 'μ' is a scalar, is `hati + (-1 - 2μ)hatj + (μ)hatk`, for some μ.

Now, the vector `vec(PQ) = vec(OQ) - vec(OP) = (1 - λ)hati + (-1 - 2μ + λ)hatj + (μ - λ)hatk`; (where 'O' is the origin), is perpendicular to both the lines, so the vector `vec(PQ)` is perpendicular to both the vectors `hati - hatj + hatk` and `-2hatj + hatk`.

`\implies` (1 – λ).1 + (–1 – 2μ + λ).(–1) + (μ – λ).1 = 0 and

`\implies` (1 – λ).0 + (–1 – 2μ + λ).(–2) + (μ – λ).1 = 0

`\implies` 2 + 3μ – 3λ = 0 and 2 + 5μ – 3λ = 0

On solving the above equations, we get λ = `2/3` and μ = 0

So, the position vector of the points, at which they should be so that the distance between them is the shortest, are `2/3(hati - hatj + hatk)` and `hati - hatj`.

`vec(PQ) = vec(OQ) - vec(OP) = 1/3hati - 1/3hatj - 2/3hatk`

and `|vec(PQ)| = sqrt((1/3)^2 + (-1/3)^2 + (-2/3)^2) = sqrt(2/3)`

The shortest distance = `sqrt(2/3)` units.

Answer 2

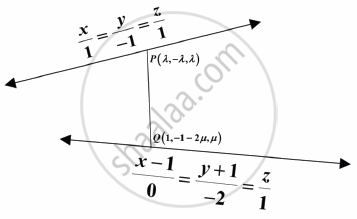
The equation of two given straight lines in the Cartesian form are

`x/1 = y/-1 = z/1`  ...(i)

and `(x - 1)/0 = (y + 1)-2 = z/1` ...(ii)

The lines are not parallel as direction ratios are not proportional. Let P be a point on straight line (i) and Q be a point on straight line (ii) such that line PQ is perpendicular to both of the lines.

Let the coordinates of P be (λ, –λ, λ) and that of Q be (1, –2μ –1, μ); where 'λ' and 'μ' are scalars.

Then the direction ratios of the line PQ are (λ – 1, –λ + 2μ + 1, λ – μ)

Since PQ is perpendicular to straight line (i), we have,

(λ – 1).1 + (–λ + 2μ + 1).(–1) + (λ – μ).1 = 0

`\implies` 3λ – 3μ = 2   ...(iii)

Since, PQ is perpendicular to straight line (ii), we have

0.(λ – 1) + (–λ + 2μ + 1).(–2) + (λ – μ).1 = 0

`\implies` 3λ – 5μ = 2   ...(iv)

Solving (iii) and (iv), we get μ = 0, λ = `2/3`

Therefore, the coordinates of P are `(2/3, -2/3, 2/3)` and that of Q are (1, –1, 0)

So, the required shortest distance is `sqrt((1 - 2/3)^2 + (-1 + 2/3)^2 + (0 - 2/3)^2) = sqrt(2/3)` units.