Advertisements
Advertisements
प्रश्न
An electron and a proton are moving under the influence of mutual forces. In calculating the change in the kinetic energy of the system during motion, one ignores the magnetic force of one on another. This is because ______.
पर्याय
the two magnetic forces are equal and opposite, so they produce no net effect.
the magnetic forces do no work on each particle.
the magnetic forces do equal and opposite (but non-zero) work on each particle.
the magenetic forces are necessarily negligible.
उत्तर
An electron and a proton are moving under the influence of mutual forces. In calculating the change in the kinetic energy of the system during motion, one ignores the magnetic force of one on another. This is because the magnetic forces do no work on each particle.
Explanation:
The work-energy theorem states that net work done equals final kinetic energy - the initial kinetic energy of the item.
The following equation demonstrates the relationship between work and kinetic energy:
∑W = K2 – K1v
As the electron and proton move under the influence of mutual interactions, the magnetic forces will be perpendicular to their motion, acting as a centripetal force for the particle.
As a result of performing the uniform circular motion in this manner, the particle's speed remains constant.
As a result, the particle's kinetic energy remains unchanged.
As a result, these forces perform no work.
`vecF_m = q(vecv xx vecB) * F_m` (magnetic force) will be perpendicular to both B and v, where B represents the external magnetic field and v represents particle velocity.
That is why the magnetic pull of one particle on another is ignored.
APPEARS IN
संबंधित प्रश्न
Is work-energy theorem valid in non-inertial frames?
A block of mass 250 g is kept on a vertical spring of spring constant 100 N/m fixed from below. The spring is now compressed 10 cm shorter than its natural length and the system is released from this position. How high does the block rise ? Take g = 10 m/s2.
The bob of a pendulum at rest is given a sharp hit to impart a horizontal velocity \[\sqrt{10 \text{ gl }}\], where l is the length of the pendulum. Find the tension in the string when (a) the string is horizontal, (b) the bob is at its highest point and (c) the string makes an angle of 60° with the upward vertical.
A simple pendulum of length L with a bob of mass m is deflected from its rest position by an angle θ and released (following figure). The string hits a peg which is fixed at a distance x below the point of suspension and the bob starts going in a circle centred at the peg. (a) Assuming that initially the bob has a height less than the peg, show that the maximum height reached by the bob equals its initial height. (b) If the pendulum is released with \[\theta = 90^\circ \text{ and x = L}/2\] , find the maximum height reached by the bob above its lowest position before the string becomes slack. (c) Find the minimum value of x/L for which the bob goes in a complete circle about the peg when the pendulum is released from \[\theta = 90^\circ \]

A particle slides on the surface of a fixed smooth sphere starting from the topmost point. Find the angle rotated by the radius through the particle, when it leaves contact with the sphere.
Figure ( following ) shows a smooth track which consists of a straight inclined part of length l joining smoothly with the circular part. A particle of mass m is projected up the incline from its bottom.Assuming that the projection-speed is only slightly greater than \[\nu_0\] , where will the block lose contact with the track?
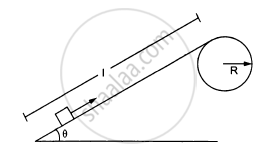
A chain of length l and mass m lies on the surface of a smooth sphere of radius R > l with one end tied to the top of the sphere. Suppose the chain is released and slides down the sphere. Find the kinetic energy of the chain, when it has slid through an angle θ.
A man, of mass m, standing at the bottom of the staircase, of height L climbs it and stands at its top.
- Work done by all forces on man is equal to the rise in potential energy mgL.
- Work done by all forces on man is zero.
- Work done by the gravitational force on man is mgL.
- The reaction force from a step does not do work because the point of application of the force does not move while the force exists.
Two bodies of unequal mass are moving in the same direction with equal kinetic energy. The two bodies are brought to rest by applying retarding force of same magnitude. How would the distance moved by them before coming to rest compare?
A raindrop of mass 1.00 g falling from a height of 1 km hits the ground with a speed of 50 ms–1. Calculate
- the loss of P.E. of the drop.
- the gain in K.E. of the drop.
- Is the gain in K.E. equal to a loss of P.E.? If not why.
Take g = 10 ms–2
