Advertisements
Advertisements
प्रश्न
Answer the following question.
Show that its time period is given by, 2π`sqrt((l cos theta)/("g"))` where l is the length of the string, θ is the angle that the string makes with the vertical, and g is the acceleration due to gravity.
उत्तर
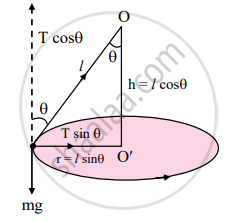
Conical pendulum
Where,
O: rigid support,
T: tension in the string,
l: length of string,
h: height of support from bob,
v: velocity of bob,
r: radius of horizontal circle,
θ: semi-vertical angle,
mg: weight of bob
- Consider a bob of mass m tied to one end of a string of length ‘l’ and the other end is fixed to a rigid support.
- Let the bob be displaced from its mean position and whirled around a horizontal circle of radius ‘r’ with constant angular velocity ω, then the bob performs U.C.M.
- During the motion, string is inclined to the vertical at an angle θ as shown in the figure above.
- In the displaced position, there are two forces acting on the bob.
a. The weight mg acting vertically downwards.
b. The tension T acting upward along the string. - The tension (T) acting in the string can be resolved into two components:
a. T cos θ acting vertically upwards.
b. T sin θ acting horizontally towards centre of the circle. - Since there is no net force, the vertical component T cos θ balances the weight and the horizontal component T sin θ provides the necessary centripetal force.
∴ T cos θ = mg ....(1)
T sin θ = `"mv"^2/"r" = "mr"omega^2` ....(2) - Dividing equation (2) by (1),
tan θ = `"v"^2/"rg"` ....(3)
Therefore, the angle made by the string with the vertical is θ = tan-1 `("v"^2/"rg")` - Since we know v = `(2pi"r")/"T"`
∴ tan θ = `(4pi^2"r"^2)/("T"^2"rg")` ....[From (3)]
T = `2pi sqrt("r"/("g"tan theta))`
T = `2pi sqrt((l sin theta)/("g"tan theta)) ....[because "r" = l sin theta]`
T = `2pi sqrt((l cos theta)/("g"))`
T = `2pi sqrt("h"/"g")` .....(∵ h = l cos θ)
where l is length of the pendulum and h is the vertical distance of the horizontal circle from the fixed point O.
APPEARS IN
संबंधित प्रश्न
A particle rotates in U.C.M. with tangential velocity V along a horizontal circle of diameter ‘D' . Total angular displacement of the particle in time 't' is..........
Draw a neat labelled diagram of conical pendulum. State the expression for its periodic time in terms of length.
A cyclist is riding with a speed of 27 km/h. As he approaches a circular turn on the road of radius 80 m, he applies brakes and reduces his speed at the constant rate of 0.50 m/s every second. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn?
| A small pebble tied at one end of a string is placed near the periphery of a circular disc, at the centre of which the other end of the string is tied to a peg. The disc is rotating about an axis passing through its centre. |
- What will be your observation when you are standing outside the disc? Explain.
- What will be your observation when you are standing at the centre of the disc? Explain.
State True or False
The earth moves around the sun with a uniform.
In a uniform circular motion, the speed continuously changes because of the direction of motion changes.
Solve the following problem.
A car moves in a circle at a constant speed of 50 m/s and completes one revolution in 40 s. Determine the magnitude of the acceleration of the car.
Which of the following graph represents uniform motion of a moving particle?
What is meant by uniform circular motion? Give two examples of uniform circular motion.
A wheel is 0.25 m in radius. When it makes 15 revolutions per minute, its linear speed at the point on circumference is ____________.
A body of mass ·m' is moving along a circle of radius 'r' with linear speed 'v'. Now, to change the linear speed to `V/2` and to move it along the circle of radius '4r', required change in the centripetal force of the body is ______.
At any instant, the magnitude of the centripetal force on a particle of mass 'm' performing circular motion is given by (ω = angular velocity and v = linear velocity of the particle) ______.
A stone of mass 3 kg attached at one end of a 2m long string is whirled in horizontal circle. The string makes an angle of 45° with the vertical then the centripetal force acting on the string is ______.
(g = 10 m/s2 , tan 45° = 1)
A body is said to be in nonuniform motion if it travels ______.
In uniform motion, an object travels equal ______ in ______ interval of time.
The motion of the bus is ______ motion.
A flywheel at rest is to reach an angular velocity of 24 rad/s in 8 second with constant angular acceleration. The total angle turned through during this interval is ______.
For a particle performing uniform circular motion, choose the correct statement(s) from the following:
- Magnitude of particle velocity (speed) remains constant.
- Particle velocity remains directed perpendicular to radius vector.
- Direction of acceleration keeps changing as particle moves.
- Angular momentum is constant in magnitude but direction keeps changing.
Earth can be thought of as a sphere of radius 6400 km. Any object (or a person) is performing circular motion around the axis of earth due to earth’s rotation (period 1 day). What is acceleration of object on the surface of the earth (at equator) towards its centre? what is it at latitude θ? How does these accelerations compare with g = 9.8 m/s2?
Earth also moves in circular orbit around sun once every year with on orbital radius of 1.5 × 1011 m. What is the acceleration of earth (or any object on the surface of the earth) towards the centre of the sun? How does this acceleration compare with g = 9.8 m/s2?
A disc of radius 5 cm rolls on a horizontal surface with linear velocity v = 1`hat"i"` m/s and angular velocity 50 rad/s. Height of particle from ground on rim of disc which has velocity in vertical direction is ______ cm.
A ceiling fan rotates about its own axis with some angular velocity. When the fan is switched off the angular velocity becomes `(1/4)^"th"` of the original in time 't' and 'n' revolutions are made in that time. The number of revolutions made by the fan during the time interval between switch off and rest are ______. (Angular retardation is uniform)
A particle moves along a circle of radius r with constant tangential acceleration. If the velocity of the particle is v at the end of second revolution, after the revolution has started, then the tangential acceleration is ______.
Angular speed of hour hand of a clock in degree per second is ______.
A wheel is Subjected to uniform angular acceleration about its axis. Initially. its angular velocity is zero. In the first 2 s, it rotates through an angle θ1, in the next 2 s, it rotates through an angle θ2. The ratio of `theta_2/theta_1` is ______.
A body of mass m is moving in circle of radius r with a constant speed v. The work done by the centripetal force in moving the body over half the circumference of the circle is ______.
Explain the meaning of uniform circular motion.
Why is uniform circular motion said to be accelerated?
