Advertisements
Advertisements
प्रश्न
Area of the region bounded by x2 = 16y, y = 1 and y = 4 and the Y-axis, lying in the first quadrant is _______.
पर्याय
63 sq. units
`(3)/(56)"sq. units"`
`(56)/(3)"sq. units"`
`(63)/(7)"sq. units"`
उत्तर
Area of the region bounded by x2 = 16y, y = 1 and y = 4 and the Y-axis, lying in the first quadrant is `bbunderline((56)/(3)"sq. units")`.
Explanation:
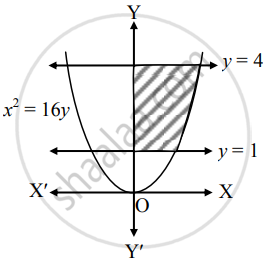
Required area = `int_1^4x*dy`
= `int_1^4 4sqrt(y)*dy`
= `4[y^(3/2)/(3/2)]_1^4`
= `(8)/(3)[(4)^(3/2) - (1)^(3/2)]`
= `(8)/(3)(8 - 1)`
= `(56)/(3)"sq.units"`.
APPEARS IN
संबंधित प्रश्न
Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32.
Find the area of the region bounded by y2 = 9x, x = 2, x = 4 and the x-axis in the first quadrant.
Find the area of the smaller region bounded by the ellipse `x^2/a^2 + y^2/b^2 = 1` and the line `x/a + y/b = 1`
Find the area of the region {(x, y) : y2 ≤ 4x, 4x2 + 4y2 ≤ 9}
Find the equation of an ellipse whose latus rectum is 8 and eccentricity is `1/3`
Draw a rough sketch and find the area bounded by the curve x2 = y and x + y = 2.
Find the area of the region bounded by the following curves, the X-axis and the given lines: 2y + x = 8, x = 2, x = 4
The area of the region bounded by y2 = 4x, the X-axis and the lines x = 1 and x = 4 is _______.
Using definite integration, area of the circle x2 + y2 = 49 is _______.
Solve the following :
Find the area of the region bounded by the curve xy = c2, the X-axis, and the lines x = c, x = 2c.
Choose the correct alternative:
Area of the region bounded by the curve y = x3, x = 1, x = 4 and the X-axis is ______
The area bounded by the parabola x2 = 9y and the lines y = 4 and y = 9 in the first quadrant is ______
Find the area of the region bounded by the curve 4y = 7x + 9, the X-axis and the lines x = 2 and x = 8
Find the area of the circle x2 + y2 = 62
The ratio in which the area bounded by the curves y2 = 8x and x2 = 8y is divided by the line x = 2 is ______
Area under the curve `y=sqrt(4x+1)` between x = 0 and x = 2 is ______.
The area enclosed by the parabolas x = y2 - 1 and x = 1 - y2 is ______.
The equation of curve through the point (1, 0), if the slope of the tangent to t e curve at any point (x, y) is `(y - 1)/(x^2 + x)`, is
Area bounded by the curves y = `"e"^(x^2)`, the x-axis and the lines x = 1, x = 2 is given to be α square units. If the area bounded by the curve y = `sqrt(ℓ "n"x)`, the x-axis and the lines x = e and x = e4 is expressed as (pe4 – qe – α), (where p and q are positive integers), then (p + q) is ______.
