Advertisements
Advertisements
प्रश्न
Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32.
Using integration, find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32.
उत्तर १
y = x ...(1)
x2 + y2 = 32 ...(2)
The region enclosed by y = x and x2 + y2 = 32 is shown in the following figure:
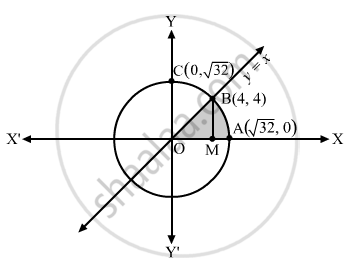
On solving (1) and (2) we find that the given line and circle meet at B(4, 4) in the first quadrant. Let us draw BM perpendicular to the x-axis.
Now, required area = area of triangle BOM + area of region BMAB
Area of triangle BOM
Area of region BMAB=
∴ Area of triangle BOM=4π−8 ... (4)
On adding (3) and (4), we have:
Required area =
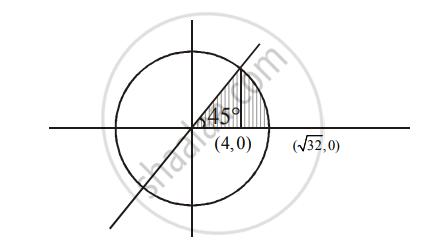
उत्तर २
Put y = x in
x = 4
APPEARS IN
संबंधित प्रश्न
Find the area of the region bounded by the ellipse
Find the area of the region bounded by the ellipse
Find the area of the smaller part of the circle x2 + y2 = a2 cut off by the line
The area between x = y2 and x = 4 is divided into two equal parts by the line x = a, find the value of a.
Find the area of the smaller region bounded by the ellipse
Using the method of integration find the area of the triangle ABC, coordinates of whose vertices are A(2, 0), B (4, 5) and C (6, 3).
Find the area of the region {(x, y) : y2 ≤ 4x, 4x2 + 4y2 ≤ 9}
Find the area bounded by the circle x2 + y2 = 16 and the line
Find the area of the region bounded by the parabola y2 = 16x and the line x = 4.
Choose the correct alternative :
Area of the region bounded by the curve x2 = y, the X-axis and the lines x = 1 and x = 3 is _______.
Solve the following :
Find the area of the region bounded by y = x2, the X-axis and x = 1, x = 4.
Solve the following:
Find the area of the region bounded by the curve x2 = 25y, y = 1, y = 4 and the Y-axis.
Choose the correct alternative:
Area of the region bounded by the curve x2 = 8y, the positive Y-axis lying in the first quadrant and the lines y = 4 and y = 9 is ______
State whether the following statement is True or False:
The area of portion lying below the X axis is negative
The area of the region x2 = 4y, y = 1 and y = 2 and the Y axis lying in the first quadrant is ______
Find the area of the region bounded by the curve y =
Find the area of the region bounded by the curve y =
Find area of the region bounded by the parabola x2 = 36y, y = 1 and y = 4, and the positive Y-axis
Find the area of the circle x2 + y2 = 62
If
The area of the region bounded by the curve y = 4x3 − 6x2 + 4x + 1 and the lines x = 1, x = 5 and X-axis is ____________.
The area of the region bounded by the X-axis and the curves defined by y = cot x,
Area under the curve
If a2 + b2 + c2 = – 2 and f(x) =
The area included between the parabolas y2 = 4a(x +a) and y2 = 4b(x – a), b > a > 0, is
The area bounded by the curve | x | + y = 1 and X-axis is ______.
