Question

Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x² + y² = 32.

Using integration, find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x² + y² = 32.

Answer 1

y = x                                           ...(1)

x² + y² = 32                                ...(2)

The region enclosed by y = x and x² + y² = 32 is shown in the following figure:

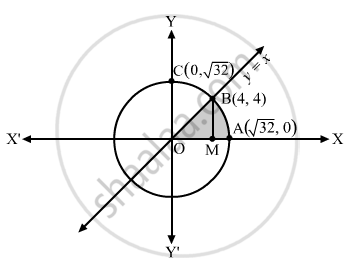
On solving (1) and (2) we find that the given line and circle meet at B(4, 4) in the first quadrant. Let us draw BM perpendicular to the x-axis.

Now, required area = area of triangle BOM + area of region BMAB

Area of triangle BOM `=int_0^4ydx=int_0^4xdx=1/2[x^2/2]_0^4=8.........(3)`

Area of region BMAB= `int_0^sqrt32ydx=int_0^sqrt32sqrt(32-x^2)`

`=[1/2xxsqrt(32-x^2)+1/2xx32xxsin^(-1)(x/sqrt32)]_4^sqrt32`

`=(1/2 xx sqrt32 xx 0+1/2xx 32 xx sin^(−1)(1))−(1/2 xx 4xx 4+1/2 xx 32 xx sin^ (−1)(1/sqrt2))`

`=8π−8−4π`

∴ Area of triangle BOM=4π−8   ... (4)

On adding (3) and (4), we have:

Required area =`8+4π−8=4π`

Answer 2

Put y = x in `x^2 + y^2 = 32`

`:. x^2  + x^2 = 32`

`2x^2 = 32`

`x^2 = 16`

x = 4

`A = int_0^4 y_"line" dx + int_4^(sqrt32) y_"circle" dx`

`A = int_0^4 xdx + int_4^(sqrt32) (sqrt(32-x^2))dx`

`= (x^2/2)_0^4 + int_4^(sqrt32) sqrt((sqrt32)^2 - x^2 )dx`

`= (8) + (x/2 sqrt(32-x^2) + 32/2 sin^(-1) (x/sqrt32))^(sqrt32)`

`= (8) + (0 + 16 xx pi/2 - (2sqrt16 + 16sin^(-1) (4/sqrt32)))`

`= 8 + 8pi - 8 - 16 sin^(-1) (1/sqrt2)`

`= 8pi - 16 xx  pi/4 =  8pi - 4pi = 4pi sq  unit`