Advertisements
Advertisements
प्रश्न
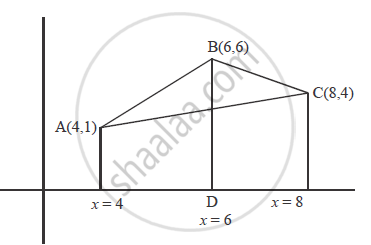
Using the method of integration, find the area of the triangle ABC, coordinates of whose vertices are A (4 , 1), B (6, 6) and C (8, 4).
उत्तर
Equation of AB
`y - y_1 = (y_2 -y_1)/(x_2-x_1) (x - x_1)`
`y - 1 = (6-1)/(6-4) (x - 4)`
`y - 1 = 5/2 (x - 4)`
2y - 2 = 5x - 20
`y = (5x)/2 - 9`
Equation of BC
`y - 6 = (4 - 6)/(8 - 6) (x - 6)`
`y - 6 = (-2)/(+2) (x - 6)`
y - 6 = -x + 6
y = -x + 12
Equation of AC
`y - 1 = (4 -1)/(8 - 4) (x - 4)`
`y -1 = 3/4 (x - 4)`
`4y - 4 = 3x - 12`
`y = (3x)/4 - 2`

संबंधित प्रश्न
Area lying in the first quadrant and bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2 is ______.
Find the area enclosed by the parabola 4y = 3x2 and the line 2y = 3x + 12
Find the area enclosed between the parabola 4y = 3x2 and the straight line 3x - 2y + 12 = 0.
Find the equation of an ellipse whose latus rectum is 8 and eccentricity is `1/3`
Using integration, find the area of the region {(x, y) : x2 + y2 ≤ 1 ≤ x + y}.
Find the area of the region.
{(x,y) : 0 ≤ y ≤ x2 , 0 ≤ y ≤ x + 2 ,-1 ≤ x ≤ 3} .
The area of the region bounded by y2 = 4x, the X-axis and the lines x = 1 and x = 4 is _______.
Area of the region bounded by x2 = 16y, y = 1 and y = 4 and the Y-axis, lying in the first quadrant is _______.
Solve the following :
Find the area of the region bounded by the curve xy = c2, the X-axis, and the lines x = c, x = 2c.
Solve the following :
Find the area of the region bounded by the curve y = x2 and the line y = 10.
Choose the correct alternative:
Area of the region bounded by the curve y = x3, x = 1, x = 4 and the X-axis is ______
Choose the correct alternative:
Area of the region bounded by x = y4, y = 1 and y = 5 and the Y-axis lying in the first quadrant is ______
State whether the following statement is True or False:
The equation of the area of the circle is `x^2/"a"^2 + y^2/"b"^2` = 1
The area of the region bounded by the curve y2 = 4x, the X axis and the lines x = 1 and x = 4 is ______
The area of the region lying in the first quadrant and bounded by the curve y = 4x2, and the lines y = 2 and y = 4 is ______
Find the area of the region bounded by the curve y = (x2 + 2)2, the X-axis and the lines x = 1 and x = 3
Find area of the region bounded by the parabola x2 = 36y, y = 1 and y = 4, and the positive Y-axis
Find the area of the region bounded by the curve y = `sqrt(36 - x^2)`, the X-axis lying in the first quadrant and the lines x = 0 and x = 6
Find the area of the circle x2 + y2 = 62
The area bounded by y = `27/x^3`, X-axis and the ordinates x = 1, x = 3 is ______
Area bounded by the curve xy = 4, X-axis between x = 1, x = 5 is ______.
Area under the curve `y=sqrt(4x+1)` between x = 0 and x = 2 is ______.
The area enclosed by the parabolas x = y2 - 1 and x = 1 - y2 is ______.
The area of the region bounded by the curve y = x IxI, X-axis and the ordinates x = 2, x = –2 is ______.
The area included between the parabolas y2 = 4a(x +a) and y2 = 4b(x – a), b > a > 0, is
The slope of a tangent to the curve y = 3x2 – x + 1 at (1, 3) is ______.
The area of the region bounded by the curve y = x2, x = 0, x = 3, and the X-axis is ______.
The area (in sq.units) of the part of the circle x2 + y2 = 36, which is outside the parabola y2 = 9x, is ______.
If the area enclosed by y = f(x), X-axis, x = a, x = b and y = g(x), X-axis, x = a, x = b are equal, then f(x) = g(x).
