Advertisements
Advertisements
प्रश्न
The area of the region bounded by y2 = 4x, the X-axis and the lines x = 1 and x = 4 is _______.
विकल्प
28 sq. units
3 sq. units
`(28)/(3)` sq. units
`(3)/(28)` sq. units
उत्तर
`bb((28)/(3))` sq. units
Explanation:
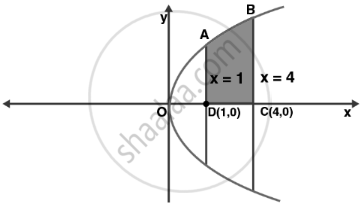
The right-handed parabola in this example, y2 = 4x, has its vertex at the origin, and the lines parallel to the y-axis at x = 1 to x = 4 units distance are x = 1, x = 4.
Similarly y2 = 4x contains even power of y and is symmetrical about the x-axis.
So the required area = Area of ABCD
Area of ABCD = `int_1^4ydx=int_1^4sqrt(4x)dx`
It can be written as
= `2int_1^4sqrtxdx`
= `2[(x3/2)/(3/2)]_1^4`
= `2[(2x3/2)/3]_1^4`
Substituting the values we get
= `2((2(4)3/2)/3-(2(1)3/2)/3)`
= `4(8/3-1/3)`
= `4(7/3)`
= `28/3` sq. units
APPEARS IN
संबंधित प्रश्न
Using integration find the area of the region {(x, y) : x2+y2⩽ 2ax, y2⩾ ax, x, y ⩾ 0}.
Area lying in the first quadrant and bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2 is ______.
Find the area under the given curve and given line:
y = x4, x = 1, x = 5 and x-axis
Find the area of the region lying in the first quadrant and bounded by y = 4x2, x = 0, y = 1 and y = 4
Find the area of the region.
{(x,y) : 0 ≤ y ≤ x2 , 0 ≤ y ≤ x + 2 ,-1 ≤ x ≤ 3} .
Area of the region bounded by x2 = 16y, y = 1 and y = 4 and the Y-axis, lying in the first quadrant is _______.
Choose the correct alternative :
Area of the region bounded by y = x4, x = 1, x = 5 and the X-axis is _____.
Using definite integration, area of the circle x2 + y2 = 49 is _______.
Solve the following :
Find the area of the region bounded by the curve xy = c2, the X-axis, and the lines x = c, x = 2c.
Solve the following:
Find the area of the region bounded by the curve x2 = 25y, y = 1, y = 4 and the Y-axis.
Choose the correct alternative:
Area of the region bounded by the curve x2 = 8y, the positive Y-axis lying in the first quadrant and the lines y = 4 and y = 9 is ______
The area of the region lying in the first quadrant and bounded by the curve y = 4x2, and the lines y = 2 and y = 4 is ______
Find the area of the region bounded by the parabola y2 = 25x and the line x = 5
Find the area of the region bounded by the curve y = (x2 + 2)2, the X-axis and the lines x = 1 and x = 3
Which equation below represents a parabola that opens upward with a vertex at (0, – 5)?
If a2 + b2 + c2 = – 2 and f(x) = `|(1 + a^2x, (1 + b^2)x, (1 + c^2)x),((1 + a^2)x, 1 + b^2x, (1 + c^2)x),((1 + a^2)x, (1 + b^2)x, 1 + c^2x)|` then f(x) is a polynomial of degree
Area of the region bounded by y= x4, x = 1, x = 5 and the X-axis is ______.
The area bounded by the curve | x | + y = 1 and X-axis is ______.
The area bounded by the curve, y = –x, X-axis, x = 1 and x = 4 is ______.
