Advertisements
Advertisements
प्रश्न
Solve the following:
Find the area of the region bounded by the curve x2 = 25y, y = 1, y = 4 and the Y-axis.
उत्तर
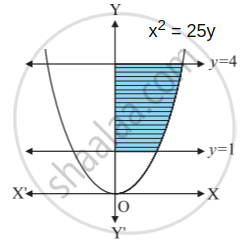
The given equation of the curve is x2 = 25y.
∴ `5sqrt(y)` ...(∵ In first quadrant, x > 0)
Required area = `int_1^4x.dy`
∴ A = `int_1^4 5sqrt(y).dy`
∴ A = `5int_1^4 y^(1/2).dy`
∴ A = `5[(y^(3/2))/(3/2)]_1^4`
∴ A = `5 × 2/3 [4^(3/2) - 1]`
∴ A = `10/3 [(2^2)^(3/2) - 1]`
∴ A = `10/3 [8 - 1]`
∴ A = `10/3 × 7`
∴ A = `70/3` sq. units
APPEARS IN
संबंधित प्रश्न
Using integration find the area of the triangle formed by positive x-axis and tangent and normal of the circle
`x^2+y^2=4 at (1, sqrt3)`
Find the area of the region bounded by the ellipse `x^2/16 + y^2/9 = 1.`
Find the area of the region bounded by the ellipse `x^2/4 + y^2/9 = 1.`
Find the area of the region {(x, y) : y2 ≤ 4x, 4x2 + 4y2 ≤ 9}
Find the equation of an ellipse whose latus rectum is 8 and eccentricity is `1/3`
Find the area of the region.
{(x,y) : 0 ≤ y ≤ x2 , 0 ≤ y ≤ x + 2 ,-1 ≤ x ≤ 3} .
Using integration find the area of the triangle formed by negative x-axis and tangent and normal to the circle `"x"^2 + "y"^2 = 9 "at" (-1,2sqrt2)`.
Using definite integration, area of the circle x2 + y2 = 49 is _______.
Solve the following :
Find the area of the region bounded by y = x2, the X-axis and x = 1, x = 4.
The area bounded by the parabola x2 = 9y and the lines y = 4 and y = 9 in the first quadrant is ______
Find the area of the region bounded by the parabola y2 = 25x and the line x = 5
Find area of the region bounded by the parabola x2 = 36y, y = 1 and y = 4, and the positive Y-axis
Find the area of the circle x2 + y2 = 62
The area bounded by y = `27/x^3`, X-axis and the ordinates x = 1, x = 3 is ______
The ratio in which the area bounded by the curves y2 = 8x and x2 = 8y is divided by the line x = 2 is ______
Area bounded by the curve xy = 4, X-axis between x = 1, x = 5 is ______.
The area (in sq. units) of the region {(x, y) : y2 ≥ 2x and x2 + y2 ≤ 4x, x ≥ 0, y ≥ 0} is ______.
The area enclosed by the parabola x2 = 4y and its latus rectum is `8/(6m)` sq units. Then the value of m is ______.
