Advertisements
Advertisements
प्रश्न
Using integration find the area of the triangle formed by negative x-axis and tangent and normal to the circle `"x"^2 + "y"^2 = 9 "at" (-1,2sqrt2)`.
उत्तर
The equation of circle is `"x"^2 + "y"^2 = 9`
∴ `2"x" + 2"y"(d"y")/(d"x") = 0`
⇒ `(d"y")/(d"x") = -("x")/("y")`
Slope of tangent at `(-1,2sqrt(2)) and "m"_"T" = (1)/(2sqrt(2)`
∴ eq. of tangent : `"y" - 2sqrt(2) = (1)/(2sqrt(2))("x"+ 1)`
⇒ `"x" - 2sqrt(2) "y" + 9 = 0`
Clearly it cuts x axis at `(-9,0)`
Also eq. of normal : `"y"-2sqrt(2) = -2sqrt(2)("x"+1)`
⇒ `2sqrt(2"x")+"y" = 0`
As tangent and normal both meet at the point `(-1,2sqrt(2))`.
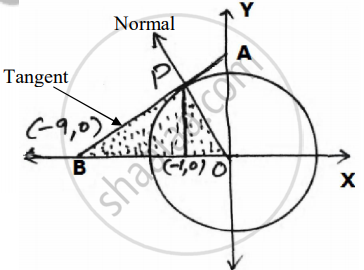
So, ar(OPB) = `int_-9^-1 ("x"+9)/(2sqrt(2))d"x" + int_-1^0 -2sqrt(2)"x"d"x"`
⇒ = `(1)/(2sqrt(2))["x"^2/(2) + 9"x"]_-9^-1 - sqrt2["x"^2/2]_-1^0`
⇒ = `(1)/(2sqrt2)[(1/2 - 9)-(81/2 - 81)]-sqrt(2)[0-1]`
∴ ar(OPB) = `9sqrt2 "sq.units"`.
APPEARS IN
संबंधित प्रश्न
Find the area of the region bounded by the curve y2 = x and the lines x = 1, x = 4 and the x-axis.
Find the area of the region bounded by the curve y2 = 4x and the line x = 3
Area lying in the first quadrant and bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2 is ______.
Draw a rough sketch and find the area bounded by the curve x2 = y and x + y = 2.
Find the area of the region bounded by the following curves, the X-axis and the given lines: 2y = 5x + 7, x = 2, x = 8
Choose the correct alternative :
Area of the region bounded by the curve x2 = y, the X-axis and the lines x = 1 and x = 3 is _______.
Area of the region bounded by x2 = 16y, y = 1 and y = 4 and the Y-axis, lying in the first quadrant is _______.
Fill in the blank :
Area of the region bounded by y = x4, x = 1, x = 5 and the X-axis is _______.
If the curve, under consideration, is below the X-axis, then the area bounded by curve, X-axis and lines x = a, x = b is positive.
Choose the correct alternative:
Using the definite integration area of the circle x2 + y2 = 16 is ______
Choose the correct alternative:
Area of the region bounded by the parabola y2 = 25x and the lines x = 5 is ______
The area of the shaded region bounded by two curves y = f(x), and y = g(x) and X-axis is `int_"a"^"b" "f"(x) "d"x + int_"a"^"b" "g"(x) "d"x`
The area bounded by the parabola x2 = 9y and the lines y = 4 and y = 9 in the first quadrant is ______
Find the area of the region bounded by the curve y = `sqrt(9 - x^2)`, X-axis and lines x = 0 and x = 3
Find the area of the region bounded by the curve y = `sqrt(2x + 3)`, the X axis and the lines x = 0 and x = 2
Find the area of the region bounded by the curve 4y = 7x + 9, the X-axis and the lines x = 2 and x = 8
Find the area of the region bounded by the curve y = (x2 + 2)2, the X-axis and the lines x = 1 and x = 3
Find area of the region bounded by 2x + 4y = 10, y = 2 and y = 4 and the Y-axis lying in the first quadrant
Find the area of the region bounded by the curve x = `sqrt(25 - y^2)`, the Y-axis lying in the first quadrant and the lines y = 0 and y = 5
The area enclosed between the curve y = loge(x + e) and the coordinate axes is ______.
Area bounded by the curve xy = 4, X-axis between x = 1, x = 5 is ______.
The area included between the parabolas y2 = 4a(x +a) and y2 = 4b(x – a), b > a > 0, is
The slope of a tangent to the curve y = 3x2 – x + 1 at (1, 3) is ______.
The area (in sq.units) of the part of the circle x2 + y2 = 36, which is outside the parabola y2 = 9x, is ______.
If area of the region bounded by y ≥ cot( cot–1|In|e|x|) and x2 + y2 – 6 |x| – 6|y| + 9 ≤ 0, is λπ, then λ is ______.
The area bounded by the x-axis and the curve y = 4x – x2 – 3 is ______.
The area enclosed by the parabola x2 = 4y and its latus rectum is `8/(6m)` sq units. Then the value of m is ______.
Find the area of the regions bounded by the line y = −2x, the X-axis and the lines x = −1 and x = 2.
