Advertisements
Advertisements
प्रश्न
Using integration find the area of the triangle formed by negative x-axis and tangent and normal to the circle `"x"^2 + "y"^2 = 9 "at" (-1,2sqrt2)`.
उत्तर
The equation of circle is `"x"^2 + "y"^2 = 9`
∴ `2"x" + 2"y"(d"y")/(d"x") = 0`
⇒ `(d"y")/(d"x") = -("x")/("y")`
Slope of tangent at `(-1,2sqrt(2)) and "m"_"T" = (1)/(2sqrt(2)`
∴ eq. of tangent : `"y" - 2sqrt(2) = (1)/(2sqrt(2))("x"+ 1)`
⇒ `"x" - 2sqrt(2) "y" + 9 = 0`
Clearly it cuts x axis at `(-9,0)`
Also eq. of normal : `"y"-2sqrt(2) = -2sqrt(2)("x"+1)`
⇒ `2sqrt(2"x")+"y" = 0`
As tangent and normal both meet at the point `(-1,2sqrt(2))`.
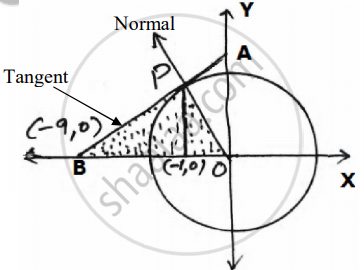
So, ar(OPB) = `int_-9^-1 ("x"+9)/(2sqrt(2))d"x" + int_-1^0 -2sqrt(2)"x"d"x"`
⇒ = `(1)/(2sqrt(2))["x"^2/(2) + 9"x"]_-9^-1 - sqrt2["x"^2/2]_-1^0`
⇒ = `(1)/(2sqrt2)[(1/2 - 9)-(81/2 - 81)]-sqrt(2)[0-1]`
∴ ar(OPB) = `9sqrt2 "sq.units"`.
APPEARS IN
संबंधित प्रश्न
Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32.
Find the area of the region bounded by x2 = 4y, y = 2, y = 4 and the y-axis in the first quadrant.
Find the area of the smaller part of the circle x2 + y2 = a2 cut off by the line `x = a/sqrt2`
Find the area of the region bounded by the parabola y = x2 and y = |x| .
Area lying in the first quadrant and bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2 is ______.
Find the area of the smaller region bounded by the ellipse `x^2/a^2 + y^2/b^2 = 1` and the line `x/a + y/b = 1`
Find the area enclosed between the parabola 4y = 3x2 and the straight line 3x - 2y + 12 = 0.
Find the equation of an ellipse whose latus rectum is 8 and eccentricity is `1/3`
Find the area of the region.
{(x,y) : 0 ≤ y ≤ x2 , 0 ≤ y ≤ x + 2 ,-1 ≤ x ≤ 3} .
Find the area of the region bounded by the following curves, the X-axis and the given lines: y = `sqrt(16 - x^2)`, x = 0, x = 4
Find the area of the region bounded by the following curves, the X-axis and the given lines: 2y = 5x + 7, x = 2, x = 8
Find the area of the region bounded by the following curves, the X-axis and the given lines: 2y + x = 8, x = 2, x = 4
State whether the following is True or False :
The area of the portion lying above the X-axis is positive.
Solve the following :
Find the area of the region bounded by y = x2, the X-axis and x = 1, x = 4.
The area of the circle x2 + y2 = 16 is ______
The area of the region x2 = 4y, y = 1 and y = 2 and the Y axis lying in the first quadrant is ______
The area of the region bounded by y2 = 25x, x = 1 and x = 2 the X axis is ______
Find the area of the region bounded by the curve y = (x2 + 2)2, the X-axis and the lines x = 1 and x = 3
Find area of the region bounded by the parabola x2 = 4y, the Y-axis lying in the first quadrant and the lines y = 3
If `int_0^(pi/2) log (cos x) "dx" = - pi/2 log 2,` then `int_0^(pi/2) log (cosec x)`dx = ?
The area of the region bounded by the curve y = 4x3 − 6x2 + 4x + 1 and the lines x = 1, x = 5 and X-axis is ____________.
Area enclosed between the curve y2(4 - x) = x3 and line x = 4 above X-axis is ______.
Which equation below represents a parabola that opens upward with a vertex at (0, – 5)?
If a2 + b2 + c2 = – 2 and f(x) = `|(1 + a^2x, (1 + b^2)x, (1 + c^2)x),((1 + a^2)x, 1 + b^2x, (1 + c^2)x),((1 + a^2)x, (1 + b^2)x, 1 + c^2x)|` then f(x) is a polynomial of degree
If area of the region bounded by y ≥ cot( cot–1|In|e|x|) and x2 + y2 – 6 |x| – 6|y| + 9 ≤ 0, is λπ, then λ is ______.
The figure shows as triangle AOB and the parabola y = x2. The ratio of the area of the triangle AOB to the area of the region AOB of the parabola y = x2 is equal to ______.
The area bounded by the curve, y = –x, X-axis, x = 1 and x = 4 is ______.
