Advertisements
Advertisements
प्रश्न
Find the area enclosed between the parabola 4y = 3x2 and the straight line 3x - 2y + 12 = 0.
उत्तर १
The given quations are
`y = (3x^2)/4` ....1
and, 3x – 2y + 12 = 0 ...(2)
Solving equation no. (1) & (2)
y = `(3x + 12)/2`

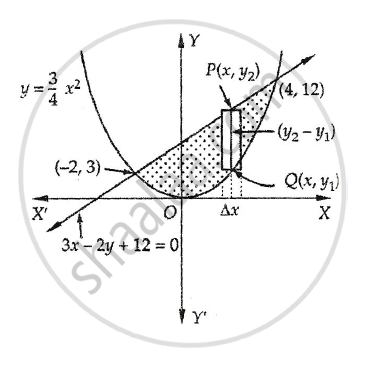
उत्तर २
The equations of the curves are
4y = 3x2 .....(1)
3x – 2y + 12 = 0 .....(2)
The curve (1) represents a parabola having vertex at the origin, axis along the positive direction of y-axis and opens upwards.
The curve (2) represents a straight line. This straight line meets the x-axis at (−4, 0) and y-axis at (0, 6).
Soving (1) and (2), we get
`3x - 2((3x^2)/4) + 12 = 0`
⇒ 6x - 3x2 + 24 = 0
⇒ x2 - 2x−8=0
⇒ (x+2)(x−4) = 0
⇒ x = -2, 4
When x = − 2, y = 3
When x = 4, y = 12
So, the point of intersection of the given curves is (− 2, 3) and (4, 12).
The area bounded by the given curves is shown below.
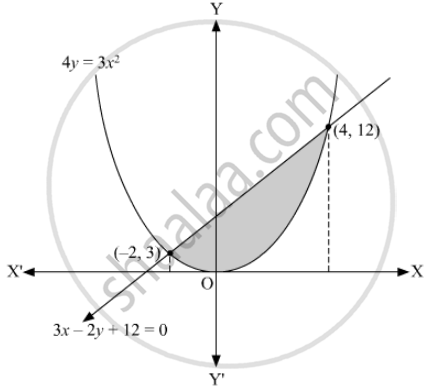
Required area = Area of the shaded region
= `int_(-2)^4 (y"Line" - y"Parabola") dx`
= `int_(-2)^4 ((3x + 12)/2 - 3/4 x^2) dx`
`= (3/4 x^2 + 6x - x^3/4)^4`
`= (3/4 xx 16 + 6 xx 4 - 64/4) - (3/4 xx 4 +6 xx (-2) + 3/4)`
= 20 - (- 7)
= 27 square units
संबंधित प्रश्न
Using integration find the area of the region {(x, y) : x2+y2⩽ 2ax, y2⩾ ax, x, y ⩾ 0}.
Find the area of the region bounded by the curve y2 = x and the lines x = 1, x = 4 and the x-axis.
Find the area bounded by the curve x2 = 4y and the line x = 4y – 2
Sketch the graph of y = |x + 3| and evaluate `int_(-6)^0 |x + 3|dx`
Find the area enclosed by the parabola 4y = 3x2 and the line 2y = 3x + 12
Find the area of the smaller region bounded by the ellipse `x^2/a^2 + y^2/b^2 = 1` and the line `x/a + y/b = 1`
Using the method of integration, find the area of the triangle ABC, coordinates of whose vertices are A (4 , 1), B (6, 6) and C (8, 4).
Find the equation of an ellipse whose latus rectum is 8 and eccentricity is `1/3`
Find the area of the region bounded by the parabola y2 = 16x and the line x = 4.
Using integration find the area of the triangle formed by negative x-axis and tangent and normal to the circle `"x"^2 + "y"^2 = 9 "at" (-1,2sqrt2)`.
Find the area of the region bounded by the following curves, the X-axis and the given lines: y = x4, x = 1, x = 5
Find the area of the region bounded by the following curves, the X-axis and the given lines: 2y + x = 8, x = 2, x = 4
Find the area of the region bounded by the parabola y2 = 4x and the line x = 3.
Using definite integration, area of the circle x2 + y2 = 49 is _______.
Solve the following :
Find the area of the region bounded by the curve xy = c2, the X-axis, and the lines x = c, x = 2c.
Choose the correct alternative:
Area of the region bounded by x = y4, y = 1 and y = 5 and the Y-axis lying in the first quadrant is ______
State whether the following statement is True or False:
The area bounded by the curve y = f(x) lies on the both sides of the X-axis is `|int_"a"^"b" "f"(x) "d"x| + |int_"b"^"c" "f"(x) "d"x|`
The area bounded by the parabola x2 = 9y and the lines y = 4 and y = 9 in the first quadrant is ______
The area of the circle x2 + y2 = 16 is ______
The area of the region bounded by the curve y2 = 4x, the X axis and the lines x = 1 and x = 4 is ______
Find the area of the region bounded by the curve 4y = 7x + 9, the X-axis and the lines x = 2 and x = 8
Find area of the region bounded by the parabola x2 = 4y, the Y-axis lying in the first quadrant and the lines y = 3
Find the area of the region bounded by the curve y = `sqrt(36 - x^2)`, the X-axis lying in the first quadrant and the lines x = 0 and x = 6
The area bounded by y = `27/x^3`, X-axis and the ordinates x = 1, x = 3 is ______
The area enclosed between the curve y = loge(x + e) and the coordinate axes is ______.
Area under the curve `y=sqrt(4x+1)` between x = 0 and x = 2 is ______.
Equation of a common tangent to the circle, x2 + y2 – 6x = 0 and the parabola, y2 = 4x, is:
The area (in sq.units) of the part of the circle x2 + y2 = 36, which is outside the parabola y2 = 9x, is ______.
The area (in sq. units) of the region {(x, y) : y2 ≥ 2x and x2 + y2 ≤ 4x, x ≥ 0, y ≥ 0} is ______.
