Advertisements
Advertisements
प्रश्न
Sketch the graph of y = |x + 3| and evaluate `int_(-6)^0 |x + 3|dx`
उत्तर
y = |x + 3|
At x = -3, y = 0
AQ is the line y = x + 3
When x + 3 < 0,
y = -(x + 3) = -x – 3
The graph of the line AP is AP.
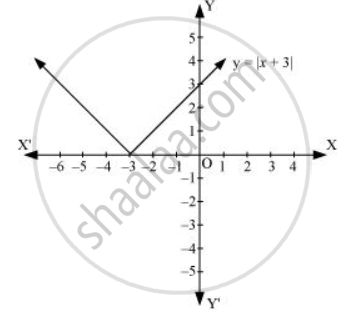
∴ y =|x + 3| is shown in the graph.
`int_(-6)^1 |x + 3| dx`
`= int_(- 6)^(-3) |- x - 3| dx + int_(-3)^0 (x + 3) dx`
`= [- x^2/2 - 3x]_(-6)^(-3) + [x^2/2 + 3x]_(- 3)^0`
`= - [x^2/2 + 3x]_(- 6)^(- 3) + [x^2/2 + 3x]_(-3)^0`
`= - [x^2/2 + 3x]_(-6)^(-3) + [x^2/2 + 3x]_(-3)^0`
`= - [(9/2 - 9) - (36/2 - 18) + 0 - (9/2 - 9)]`
`= - [- 9/2 - 0] + 9/2`
`= 9/2 + 9/2`
= 9 square unit
APPEARS IN
संबंधित प्रश्न
Find the area bounded by the curve x2 = 4y and the line x = 4y – 2
Find the area under the given curve and given line:
y = x2, x = 1, x = 2 and x-axis
Find the area under the given curve and given line:
y = x4, x = 1, x = 5 and x-axis
Find the area of the region lying in the first quadrant and bounded by y = 4x2, x = 0, y = 1 and y = 4
Find the area of the smaller region bounded by the ellipse `x^2/a^2 + y^2/b^2 = 1` and the line `x/a + y/b = 1`
Find the area enclosed between the parabola 4y = 3x2 and the straight line 3x - 2y + 12 = 0.
Find the area of the region bounded by the parabola y2 = 16x and the line x = 4.
Draw a rough sketch and find the area bounded by the curve x2 = y and x + y = 2.
Find the area of the region.
{(x,y) : 0 ≤ y ≤ x2 , 0 ≤ y ≤ x + 2 ,-1 ≤ x ≤ 3} .
Find the area of the region bounded by the following curves, the X-axis, and the given lines:
y = `sqrt(6x + 4), x = 0, x = 2`
Find the area of the region bounded by the following curves, the X-axis and the given lines: y = `sqrt(16 - x^2)`, x = 0, x = 4
Find the area of the region bounded by the following curves, the X-axis and the given lines: 2y = 5x + 7, x = 2, x = 8
Find the area of the region bounded by the following curves, the X-axis and the given lines:
y = x2 + 1, x = 0, x = 3
Find the area of the region bounded by the parabola y2 = 4x and the line x = 3.
The area of the region bounded by y2 = 4x, the X-axis and the lines x = 1 and x = 4 is _______.
Fill in the blank :
Area of the region bounded by y = x4, x = 1, x = 5 and the X-axis is _______.
Using definite integration, area of the circle x2 + y2 = 49 is _______.
If the curve, under consideration, is below the X-axis, then the area bounded by curve, X-axis and lines x = a, x = b is positive.
Solve the following :
Find the area of the region bounded by y = x2, the X-axis and x = 1, x = 4.
The area bounded by the parabola x2 = 9y and the lines y = 4 and y = 9 in the first quadrant is ______
The area of the region lying in the first quadrant and bounded by the curve y = 4x2, and the lines y = 2 and y = 4 is ______
Find the area of the region bounded by the curve y = `sqrt(9 - x^2)`, X-axis and lines x = 0 and x = 3
Find the area of the region bounded by the curve y = `sqrt(36 - x^2)`, the X-axis lying in the first quadrant and the lines x = 0 and x = 6
Find the area of the circle x2 + y2 = 62
The area enclosed between the curve y = loge(x + e) and the coordinate axes is ______.
`int "e"^x ((sqrt(1 - x^2) * sin^-1 x + 1)/sqrt(1 - x^2))`dx = ________.
Area bounded by the curve xy = 4, X-axis between x = 1, x = 5 is ______.
Area under the curve `y=sqrt(4x+1)` between x = 0 and x = 2 is ______.
The area bounded by the X-axis, the curve y = f(x) and the lines x = 1, x = b is equal to `sqrt("b"^2 + 1) - sqrt(2)` for all b > 1, then f(x) is ______.
The equation of curve through the point (1, 0), if the slope of the tangent to t e curve at any point (x, y) is `(y - 1)/(x^2 + x)`, is
The area included between the parabolas y2 = 4a(x +a) and y2 = 4b(x – a), b > a > 0, is
Find the area between the two curves (parabolas)
y2 = 7x and x2 = 7y.
The area (in sq.units) of the part of the circle x2 + y2 = 36, which is outside the parabola y2 = 9x, is ______.
Area in first quadrant bounded by y = 4x2, x = 0, y = 1 and y = 4 is ______.
The area bounded by the curve | x | + y = 1 and X-axis is ______.
Find the area of the region lying in the first quadrant and bounded by y = 4x2, x = 0,y = 2 and y = 4.
