Advertisements
Advertisements
Question
Sketch the graph of y = |x + 3| and evaluate `int_(-6)^0 |x + 3|dx`
Advertisements
Solution
y = |x + 3|
At x = -3, y = 0
AQ is the line y = x + 3
When x + 3 < 0,
y = -(x + 3) = -x – 3
The graph of the line AP is AP.
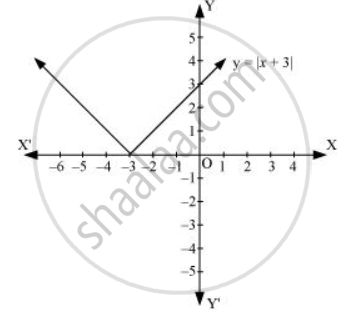
∴ y =|x + 3| is shown in the graph.
`int_(-6)^1 |x + 3| dx`
`= int_(- 6)^(-3) |- x - 3| dx + int_(-3)^0 (x + 3) dx`
`= [- x^2/2 - 3x]_(-6)^(-3) + [x^2/2 + 3x]_(- 3)^0`
`= - [x^2/2 + 3x]_(- 6)^(- 3) + [x^2/2 + 3x]_(-3)^0`
`= - [x^2/2 + 3x]_(-6)^(-3) + [x^2/2 + 3x]_(-3)^0`
`= - [(9/2 - 9) - (36/2 - 18) + 0 - (9/2 - 9)]`
`= - [- 9/2 - 0] + 9/2`
`= 9/2 + 9/2`
= 9 square unit
APPEARS IN
RELATED QUESTIONS
Find the area of the region bounded by the curve y2 = x and the lines x = 1, x = 4 and the x-axis.
Find the area of the region bounded by x2 = 4y, y = 2, y = 4 and the y-axis in the first quadrant.
Find the area bounded by the curve x2 = 4y and the line x = 4y – 2
Find the area under the given curve and given line:
y = x4, x = 1, x = 5 and x-axis
Find the area enclosed between the parabola y2 = 4ax and the line y = mx
Find the area enclosed by the parabola 4y = 3x2 and the line 2y = 3x + 12
Find the area of the region {(x, y) : y2 ≤ 4x, 4x2 + 4y2 ≤ 9}
Find the area bounded by the circle x2 + y2 = 16 and the line `sqrt3 y = x` in the first quadrant, using integration.
Find the area of the region bounded by the following curve, the X-axis and the given line:
y = 2 – x2, x = –1, x = 1
Fill in the blank :
Area of the region bounded by x2 = 16y, y = 1, y = 4 and the Y-axis, lying in the first quadrant is _______.
Find the area of the region bounded by y = x2, the X-axis and x = 1, x = 4.
Solve the following:
Find the area of the region bounded by the curve x2 = 25y, y = 1, y = 4 and the Y-axis.
Choose the correct alternative:
Area of the region bounded by the curve y = x3, x = 1, x = 4 and the X-axis is ______
Choose the correct alternative:
Area of the region bounded by the curve x2 = 8y, the positive Y-axis lying in the first quadrant and the lines y = 4 and y = 9 is ______
Choose the correct alternative:
Area of the region bounded by y2 = 16x, x = 1 and x = 4 and the X axis, lying in the first quadrant is ______
Choose the correct alternative:
Area of the region bounded by the parabola y2 = 25x and the lines x = 5 is ______
State whether the following statement is True or False:
The area bounded by the curve y = f(x) lies on the both sides of the X-axis is `|int_"a"^"b" "f"(x) "d"x| + |int_"b"^"c" "f"(x) "d"x|`
The area bounded by the parabola x2 = 9y and the lines y = 4 and y = 9 in the first quadrant is ______
The area of the region bounded by the curve y2 = 4x, the X axis and the lines x = 1 and x = 4 is ______
If `int_0^(pi/2) log (cos x) "dx" = - pi/2 log 2,` then `int_0^(pi/2) log (cosec x)`dx = ?
The area of the region bounded by the curve y = 4x3 − 6x2 + 4x + 1 and the lines x = 1, x = 5 and X-axis is ____________.
The area enclosed between the curve y = loge(x + e) and the coordinate axes is ______.
`int_0^log5 (e^xsqrt(e^x - 1))/(e^x + 3)` dx = ______
The ratio in which the area bounded by the curves y2 = 8x and x2 = 8y is divided by the line x = 2 is ______
`int "e"^x ((sqrt(1 - x^2) * sin^-1 x + 1)/sqrt(1 - x^2))`dx = ________.
The area enclosed by the parabolas x = y2 - 1 and x = 1 - y2 is ______.
Equation of a common tangent to the circle, x2 + y2 – 6x = 0 and the parabola, y2 = 4x, is:
The area of the circle `x^2 + y^2 = 16`, exterior to the parabola `y = 6x`
The area of the region bounded by the curve y = x2, x = 0, x = 3, and the X-axis is ______.
Find the area between the two curves (parabolas)
y2 = 7x and x2 = 7y.
The area of the region bounded by the curve y = sin x and the x-axis in [–π, π] is ______.
Area bounded by y = sec2x, x = `π/6`, x = `π/3` and x-axis is ______.
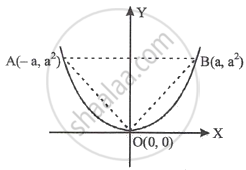
The figure shows as triangle AOB and the parabola y = x2. The ratio of the area of the triangle AOB to the area of the region AOB of the parabola y = x2 is equal to ______.
The area enclosed by the parabola x2 = 4y and its latus rectum is `8/(6m)` sq units. Then the value of m is ______.
Find the area of the regions bounded by the line y = −2x, the X-axis and the lines x = −1 and x = 2.
