Advertisements
Advertisements
Question
Draw a rough sketch and find the area bounded by the curve x2 = y and x + y = 2.
Solution
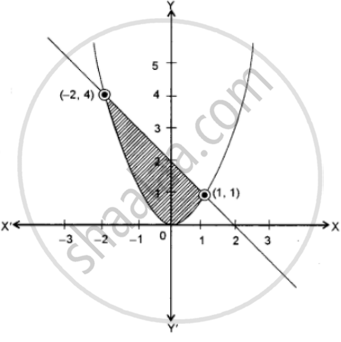
The given curves are: x2 = y
Which is an upward parabola with vertex at origin
And line x + y = 2 ⇒ y = 2 – x
x2 = 2 – x
⇒ x2 + x – 2 = 0
⇒ (x + 2)(x – 1) = 0
⇒ x = -2 and x = 1
Now, y = 2-(-2) = 4
and y = 2 – 1 ⇒ y = 1
⇒ y = 4 and y = 1
Thus, the points of intersection are (-2, 4) and (1, 1)
The required area of the shaded region
`= int_-2^1 (2 - "x") "dx" - int_-2^1 "x"^2 "dx"`
`= |2"x" - "x"^2/2|_-2^1 - |"x"^3/3|_-2^1`
`= 2 - 1/2 + 4 + 4/2 - 1/3 - 8/3`
`= (12 - 3 + 24 + 12 - 2 - 16)/6`
`= 9/2` sq.units
APPEARS IN
RELATED QUESTIONS
Find the area of the region bounded by the curve y2 = x and the lines x = 1, x = 4 and the x-axis.
Find the area of the region bounded by y2 = 9x, x = 2, x = 4 and the x-axis in the first quadrant.
Find the area of the region bounded by the ellipse `x^2/16 + y^2/9 = 1.`
The area between x = y2 and x = 4 is divided into two equal parts by the line x = a, find the value of a.
Find the area between the curves y = x and y = x2
Find the area of the region lying in the first quadrant and bounded by y = 4x2, x = 0, y = 1 and y = 4
Find the area of the smaller region bounded by the ellipse `x^2/9 + y^2/4` and the line `x/3 + y/2 = 1`
Find the area of the region {(x, y) : y2 ≤ 4x, 4x2 + 4y2 ≤ 9}
Find the area of the smaller region bounded by the ellipse \[\frac{x^2}{9} + \frac{y^2}{4} = 1\] and the line \[\frac{x}{3} + \frac{y}{2} = 1 .\]
Find the area of the region bounded by the parabola y2 = 16x and the line x = 4.
Find the area of the region bounded by the following curves, the X-axis, and the given lines:
y = `sqrt(6x + 4), x = 0, x = 2`
Find the area of the region bounded by the parabola y2 = 4x and the line x = 3.
Area of the region bounded by x2 = 16y, y = 1 and y = 4 and the Y-axis, lying in the first quadrant is _______.
If the curve, under consideration, is below the X-axis, then the area bounded by curve, X-axis and lines x = a, x = b is positive.
Solve the following :
Find the area of the region bounded by y = x2, the X-axis and x = 1, x = 4.
Solve the following:
Find the area of the region bounded by the curve x2 = 25y, y = 1, y = 4 and the Y-axis.
Choose the correct alternative:
Using the definite integration area of the circle x2 + y2 = 16 is ______
Choose the correct alternative:
Area of the region bounded by the parabola y2 = 25x and the lines x = 5 is ______
State whether the following statement is True or False:
The area of portion lying below the X axis is negative
The area of the region lying in the first quadrant and bounded by the curve y = 4x2, and the lines y = 2 and y = 4 is ______
The area of the region x2 = 4y, y = 1 and y = 2 and the Y axis lying in the first quadrant is ______
The area of the region bounded by the curve y = 4x3 − 6x2 + 4x + 1 and the lines x = 1, x = 5 and X-axis is ____________.
Area enclosed between the curve y2(4 - x) = x3 and line x = 4 above X-axis is ______.
The area of the region bounded by the X-axis and the curves defined by y = cot x, `(pi/6 ≤ x ≤ pi/4)` is ______.
The area bounded by the X-axis, the curve y = f(x) and the lines x = 1, x = b is equal to `sqrt("b"^2 + 1) - sqrt(2)` for all b > 1, then f(x) is ______.
The area of the region bounded by the curve y = x2, x = 0, x = 3, and the X-axis is ______.
The area (in sq.units) of the part of the circle x2 + y2 = 36, which is outside the parabola y2 = 9x, is ______.
The area (in sq. units) of the region {(x, y) : y2 ≥ 2x and x2 + y2 ≤ 4x, x ≥ 0, y ≥ 0} is ______.
Find the area of the region lying in the first quadrant and bounded by y = 4x2, x = 0,y = 2 and y = 4.
