Advertisements
Advertisements
Question
Find the area of the region bounded by the parabola y2 = 16x and the line x = 4.
Solution
The region bounded by the parabola `y^2` = 16x and
the line x = 4 is the area OACO
The area OACO is symmetrical about x-axis
Area of OACO = 2(Area of OAB)
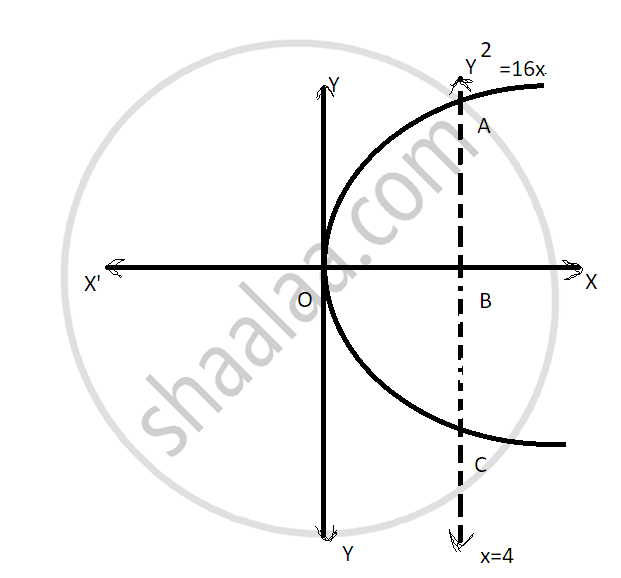
Area of OACO = `2int_0^4y dx`
=`2int_0^4 4sqrtx dx`
=`8[x^(3/2 )/(3/2)]_0^4`
=`16/3[x^(3/2)]_0^4`
=`16/3(8)=128/3`
Therefore, the required area is `128/3`sq. units.
APPEARS IN
RELATED QUESTIONS
Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32.
Using integration find the area of the triangle formed by positive x-axis and tangent and normal of the circle
`x^2+y^2=4 at (1, sqrt3)`
Find the area of the region bounded by the ellipse `x^2/4 + y^2/9 = 1.`
Find the area of the region bounded by the parabola y = x2 and y = |x| .
Find the area bounded by the curve x2 = 4y and the line x = 4y – 2
Find the area of the region bounded by the curve y2 = 4x and the line x = 3
Find the area of the region bounded by the following curves, the X-axis and the given lines: 2y + x = 8, x = 2, x = 4
Find the area of the region bounded by the following curves, the X-axis and the given lines:
y = x2 + 1, x = 0, x = 3
Fill in the blank :
Area of the region bounded by x2 = 16y, y = 1, y = 4 and the Y-axis, lying in the first quadrant is _______.
State whether the following is True or False :
The area bounded by the curve x = g (y), Y-axis and bounded between the lines y = c and y = d is given by `int_"c"^"d"x*dy = int_(y = "c")^(y = "d") "g"(y)*dy`
State whether the following is True or False :
The area of the portion lying above the X-axis is positive.
Area of the region bounded by the curve x = y2, the positive Y axis and the lines y = 1 and y = 3 is ______
Choose the correct alternative:
Area of the region bounded by x = y4, y = 1 and y = 5 and the Y-axis lying in the first quadrant is ______
The area of the region lying in the first quadrant and bounded by the curve y = 4x2, and the lines y = 2 and y = 4 is ______
Find the area of the circle x2 + y2 = 62
The area enclosed by the parabolas x = y2 - 1 and x = 1 - y2 is ______.
The area bounded by the X-axis, the curve y = f(x) and the lines x = 1, x = b is equal to `sqrt("b"^2 + 1) - sqrt(2)` for all b > 1, then f(x) is ______.
The area of the region bounded by the curve y = x IxI, X-axis and the ordinates x = 2, x = –2 is ______.
If the area enclosed by y = f(x), X-axis, x = a, x = b and y = g(x), X-axis, x = a, x = b are equal, then f(x) = g(x).
