Question

Using integration find the area of the triangle formed by positive x-axis and tangent and normal of the circle

`x^2+y^2=4 at (1, sqrt3)`

Answer 1

The given equation of the circle is x²+y²=4.

The equation of the normal to the circle at (1,√3) is same as the line joining the points (1,√3) and (0, 0), which is given by

`(y−sqrt3)/x−1=(sqrt3−0)/(1−0)`

`(y−sqrt3)/x−1=sqrt3`

`⇒y−sqrt3=sqrt3x−sqrt3`

`⇒y=sqrt3x                    .....(1)`

So, the slope of normal is `sqrt3.`

We know that the product of the slopes of the normal and the tangent is −1

Therefore, the slope of tangent is `−1/sqrt3`

Now, the equation of the tangent to the circle at (1,√3) is given by

`(y−sqrt3)/x−1=-1/sqrt3`

`⇒sqrt3y−3=−x+1`

⇒y=−(x+4)/sqrt3          .....(2)

Putting y = 0 in (2), we get x = 4.

Thus, ABC is the triangle formed by the positive x-axis and tangent and normal to the given circle at `(1,sqrt3)`

.

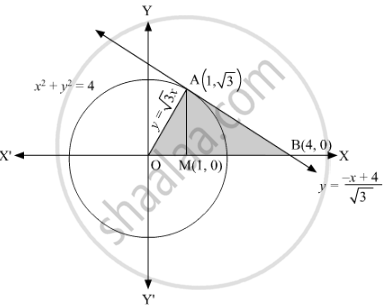
Now,

Area of ∆AOB = Area of ∆AOM + Area of ∆AMB

`=int_0^1ydx+int_1^4y dx`

`=int_0^1sqrt3xdx+int_1^4((-x+4)/sqrt3)dx`

`=[(sqrt3x^2)/2]_0^1+int_1^4-x/sqrt3dx+int_1^44/sqrt3dx`

`=(sqrt3/2-0)-[x^2/(2sqrt3)]_1^4+[4/sqrt3x]_1^4`

`=sqrt3/2-16/(2sqrt3)+1/(2sqrt3)+16/sqrt3-4/sqrt3`

`=sqrt3/2+(3sqrt3)/2`

`=2sqrt3`

Thus, the area of the triangle so formed is `2sqrt3` square units.