Advertisements
Advertisements
Question
Area of the region bounded by x2 = 16y, y = 1 and y = 4 and the Y-axis, lying in the first quadrant is _______.
Options
63 sq. units
`(3)/(56)"sq. units"`
`(56)/(3)"sq. units"`
`(63)/(7)"sq. units"`
Solution
Area of the region bounded by x2 = 16y, y = 1 and y = 4 and the Y-axis, lying in the first quadrant is `bbunderline((56)/(3)"sq. units")`.
Explanation:
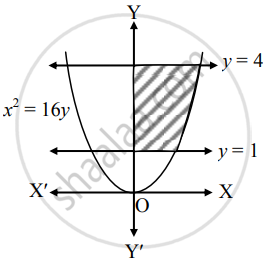
Required area = `int_1^4x*dy`
= `int_1^4 4sqrt(y)*dy`
= `4[y^(3/2)/(3/2)]_1^4`
= `(8)/(3)[(4)^(3/2) - (1)^(3/2)]`
= `(8)/(3)(8 - 1)`
= `(56)/(3)"sq.units"`.
APPEARS IN
RELATED QUESTIONS
Find the area of the region in the first quadrant enclosed by x-axis, line x = `sqrt3` y and the circle x2 + y2 = 4.
Find the area of the smaller part of the circle x2 + y2 = a2 cut off by the line `x = a/sqrt2`
The area between x = y2 and x = 4 is divided into two equal parts by the line x = a, find the value of a.
Find the area bounded by the curve x2 = 4y and the line x = 4y – 2
Find the area of the smaller region bounded by the ellipse `x^2/a^2 + y^2/b^2 = 1` and the line `x/a + y/b = 1`
Find the area of the region enclosed by the parabola x2 = y, the line y = x + 2 and x-axis
Find the area of the smaller region bounded by the ellipse \[\frac{x^2}{9} + \frac{y^2}{4} = 1\] and the line \[\frac{x}{3} + \frac{y}{2} = 1 .\]
Find the area of the region bounded by the following curves, the X-axis and the given lines: 2y + x = 8, x = 2, x = 4
Fill in the blank :
Area of the region bounded by y = x4, x = 1, x = 5 and the X-axis is _______.
The area bounded by the parabola x2 = 9y and the lines y = 4 and y = 9 in the first quadrant is ______
The area of the circle x2 + y2 = 16 is ______
Find area of the region bounded by the parabola x2 = 4y, the Y-axis lying in the first quadrant and the lines y = 3
Find the area of the circle x2 + y2 = 16
The area enclosed between the curve y = loge(x + e) and the coordinate axes is ______.
Equation of a common tangent to the circle, x2 + y2 – 6x = 0 and the parabola, y2 = 4x, is:
The area of the circle `x^2 + y^2 = 16`, exterior to the parabola `y = 6x`
If area of the region bounded by y ≥ cot( cot–1|In|e|x|) and x2 + y2 – 6 |x| – 6|y| + 9 ≤ 0, is λπ, then λ is ______.
If the area enclosed by y = f(x), X-axis, x = a, x = b and y = g(x), X-axis, x = a, x = b are equal, then f(x) = g(x).
