Advertisements
Advertisements
Question
Find the area of the smaller region bounded by the ellipse `x^2/9 + y^2/4` and the line `x/3 + y/2 = 1`
Solution
The area of the smaller region bounded by the ellipse, `x^2/9 + y^2/4` , and the line, `x/3 + y/2 = 1`, is represented by the shaded region BCAB as
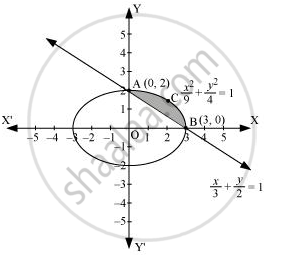
∴ Area BCAB = Area (OBCAO) – Area (OBAO)

APPEARS IN
RELATED QUESTIONS
Using integration find the area of the region {(x, y) : x2+y2⩽ 2ax, y2⩾ ax, x, y ⩾ 0}.
Using integration find the area of the triangle formed by positive x-axis and tangent and normal of the circle
`x^2+y^2=4 at (1, sqrt3)`
Find the area of the region in the first quadrant enclosed by x-axis, line x = `sqrt3` y and the circle x2 + y2 = 4.
Find the area bounded by the curve x2 = 4y and the line x = 4y – 2
Sketch the graph of y = |x + 3| and evaluate `int_(-6)^0 |x + 3|dx`
Find the area enclosed between the parabola y2 = 4ax and the line y = mx
Find the area enclosed by the parabola 4y = 3x2 and the line 2y = 3x + 12
Find the area bounded by the circle x2 + y2 = 16 and the line `sqrt3 y = x` in the first quadrant, using integration.
Find the area of the smaller region bounded by the ellipse \[\frac{x^2}{9} + \frac{y^2}{4} = 1\] and the line \[\frac{x}{3} + \frac{y}{2} = 1 .\]
Find the area of the region bounded by the following curves, the X-axis and the given lines: y = `sqrt(16 - x^2)`, x = 0, x = 4
Find the area of the region bounded by the following curves, the X-axis and the given lines: 2y + x = 8, x = 2, x = 4
Fill in the blank :
Area of the region bounded by y = x4, x = 1, x = 5 and the X-axis is _______.
Using definite integration, area of the circle x2 + y2 = 49 is _______.
Fill in the blank :
Area of the region bounded by x2 = 16y, y = 1, y = 4 and the Y-axis, lying in the first quadrant is _______.
The area of the region bounded by y2 = 4x, the X-axis and the lines x = 1 and x = 4 is _______.
State whether the following is True or False :
The area of the portion lying above the X-axis is positive.
Solve the following :
Find the area of the region bounded by the curve y = x2 and the line y = 10.
Solve the following :
Find the area of the region bounded by y = x2, the X-axis and x = 1, x = 4.
Choose the correct alternative:
Using the definite integration area of the circle x2 + y2 = 16 is ______
Area of the region bounded by the curve x = y2, the positive Y axis and the lines y = 1 and y = 3 is ______
Choose the correct alternative:
Area of the region bounded by the curve x2 = 8y, the positive Y-axis lying in the first quadrant and the lines y = 4 and y = 9 is ______
The area of the region lying in the first quadrant and bounded by the curve y = 4x2, and the lines y = 2 and y = 4 is ______
The area of the region bounded by y2 = 25x, x = 1 and x = 2 the X axis is ______
Find the area of the region bounded by the curve y = `sqrt(9 - x^2)`, X-axis and lines x = 0 and x = 3
Find area of the region bounded by 2x + 4y = 10, y = 2 and y = 4 and the Y-axis lying in the first quadrant
Find the area of the region bounded by the curve x = `sqrt(25 - y^2)`, the Y-axis lying in the first quadrant and the lines y = 0 and y = 5
Find the area of the circle x2 + y2 = 62
If `int_0^(pi/2) log (cos x) "dx" = - pi/2 log 2,` then `int_0^(pi/2) log (cosec x)`dx = ?
The area enclosed between the curve y = loge(x + e) and the coordinate axes is ______.
The equation of curve through the point (1, 0), if the slope of the tangent to t e curve at any point (x, y) is `(y - 1)/(x^2 + x)`, is
If a2 + b2 + c2 = – 2 and f(x) = `|(1 + a^2x, (1 + b^2)x, (1 + c^2)x),((1 + a^2)x, 1 + b^2x, (1 + c^2)x),((1 + a^2)x, (1 + b^2)x, 1 + c^2x)|` then f(x) is a polynomial of degree
The area of the region bounded by the curve y = x2, x = 0, x = 3, and the X-axis is ______.
Find the area between the two curves (parabolas)
y2 = 7x and x2 = 7y.
Area in first quadrant bounded by y = 4x2, x = 0, y = 1 and y = 4 is ______.
Area bounded by the curves y = `"e"^(x^2)`, the x-axis and the lines x = 1, x = 2 is given to be α square units. If the area bounded by the curve y = `sqrt(ℓ "n"x)`, the x-axis and the lines x = e and x = e4 is expressed as (pe4 – qe – α), (where p and q are positive integers), then (p + q) is ______.
The area bounded by the x-axis and the curve y = 4x – x2 – 3 is ______.
The area (in sq. units) of the region {(x, y) : y2 ≥ 2x and x2 + y2 ≤ 4x, x ≥ 0, y ≥ 0} is ______.
Find the area of the region lying in the first quadrant and bounded by y = 4x2, x = 0,y = 2 and y = 4.
Find the area of the regions bounded by the line y = −2x, the X-axis and the lines x = −1 and x = 2.
