Advertisements
Advertisements
Question
Find the area enclosed by the parabola 4y = 3x2 and the line 2y = 3x + 12
Solution
The area enclosed between the parabola, 4y = 3x2, and the line, 2y = 3x + 12, is represented by the shaded area OBAO as
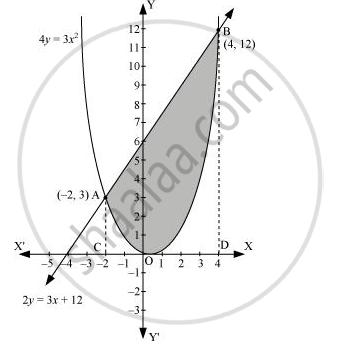
The points of intersection of the given curves are A (–2, 3) and (4, 12).
We draw AC and BD perpendicular to x-axis.
∴ Area OBAO = Area CDBA – (Area ODBO + Area OACO)
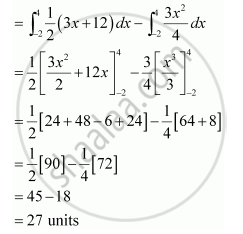
APPEARS IN
RELATED QUESTIONS
Find the area of the region bounded by the ellipse `x^2/4 + y^2/9 = 1.`
Find the area of the region bounded by the parabola y = x2 and y = |x| .
Find the area under the given curve and given line:
y = x2, x = 1, x = 2 and x-axis
Find the area enclosed between the parabola y2 = 4ax and the line y = mx
Find the area of the smaller region bounded by the ellipse `x^2/9 + y^2/4` and the line `x/3 + y/2 = 1`
Using the method of integration find the area of the triangle ABC, coordinates of whose vertices are A(2, 0), B (4, 5) and C (6, 3).
Find the area of the region {(x, y) : y2 ≤ 4x, 4x2 + 4y2 ≤ 9}
Using the method of integration, find the area of the triangle ABC, coordinates of whose vertices are A (4 , 1), B (6, 6) and C (8, 4).
Find the equation of an ellipse whose latus rectum is 8 and eccentricity is `1/3`
Draw a rough sketch and find the area bounded by the curve x2 = y and x + y = 2.
Find the area of the region bounded by the following curve, the X-axis and the given line:
y = 2 – x2, x = –1, x = 1
Find the area of the region bounded by the parabola y2 = 4x and the line x = 3.
Area of the region bounded by x2 = 16y, y = 1 and y = 4 and the Y-axis, lying in the first quadrant is _______.
Fill in the blank :
Area of the region bounded by x2 = 16y, y = 1, y = 4 and the Y-axis, lying in the first quadrant is _______.
Fill in the blank :
The area of the region bounded by the curve x2 = y, the X-axis and the lines x = 3 and x = 9 is _______.
If the curve, under consideration, is below the X-axis, then the area bounded by curve, X-axis and lines x = a, x = b is positive.
State whether the following is True or False :
The area of the portion lying above the X-axis is positive.
Solve the following :
Find the area of the region bounded by the curve xy = c2, the X-axis, and the lines x = c, x = 2c.
The area of the shaded region bounded by two curves y = f(x), and y = g(x) and X-axis is `int_"a"^"b" "f"(x) "d"x + int_"a"^"b" "g"(x) "d"x`
The area bounded by the parabola x2 = 9y and the lines y = 4 and y = 9 in the first quadrant is ______
The area of the region lying in the first quadrant and bounded by the curve y = 4x2, and the lines y = 2 and y = 4 is ______
Find the area of the region bounded by the curve y = `sqrt(9 - x^2)`, X-axis and lines x = 0 and x = 3
Find the area of the region bounded by the curve y = `sqrt(2x + 3)`, the X axis and the lines x = 0 and x = 2
Find area of the region bounded by 2x + 4y = 10, y = 2 and y = 4 and the Y-axis lying in the first quadrant
Find area of the region bounded by the parabola x2 = 36y, y = 1 and y = 4, and the positive Y-axis
`int "e"^x ((sqrt(1 - x^2) * sin^-1 x + 1)/sqrt(1 - x^2))`dx = ________.
Area bounded by the curve xy = 4, X-axis between x = 1, x = 5 is ______.
If a2 + b2 + c2 = – 2 and f(x) = `|(1 + a^2x, (1 + b^2)x, (1 + c^2)x),((1 + a^2)x, 1 + b^2x, (1 + c^2)x),((1 + a^2)x, (1 + b^2)x, 1 + c^2x)|` then f(x) is a polynomial of degree
The area of the circle `x^2 + y^2 = 16`, exterior to the parabola `y = 6x`
The area of the region bounded by the curve y = x2, x = 0, x = 3, and the X-axis is ______.
Find the area between the two curves (parabolas)
y2 = 7x and x2 = 7y.
The area of the region bounded by the curve y = sin x and the x-axis in [–π, π] is ______.
If area of the region bounded by y ≥ cot( cot–1|In|e|x|) and x2 + y2 – 6 |x| – 6|y| + 9 ≤ 0, is λπ, then λ is ______.
The area bounded by the curve | x | + y = 1 and X-axis is ______.
Find the area of the region lying in the first quadrant and bounded by y = 4x2, x = 0,y = 2 and y = 4.
