Advertisements
Advertisements
Question
Choose the correct alternative:
Area of the region bounded by the curve x2 = 8y, the positive Y-axis lying in the first quadrant and the lines y = 4 and y = 9 is ______
Options
`(76sqrt(2))/3` sq.units
`(76sqrt(2))/2` sq.units
`(38sqrt(2))/3` sq.units
`76sqrt(2)` sq.units
Solution
`(76sqrt(2))/3` sq.units
APPEARS IN
RELATED QUESTIONS
Using integration find the area of the region {(x, y) : x2+y2⩽ 2ax, y2⩾ ax, x, y ⩾ 0}.
Using integration find the area of the triangle formed by positive x-axis and tangent and normal of the circle
`x^2+y^2=4 at (1, sqrt3)`
Find the area of the region bounded by the ellipse `x^2/4 + y^2/9 = 1.`
The area between x = y2 and x = 4 is divided into two equal parts by the line x = a, find the value of a.
Area lying in the first quadrant and bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2 is ______.
Find the area of the region.
{(x,y) : 0 ≤ y ≤ x2 , 0 ≤ y ≤ x + 2 ,-1 ≤ x ≤ 3} .
Choose the correct alternative :
Area of the region bounded by y = x4, x = 1, x = 5 and the X-axis is _____.
Choose the correct alternative:
Area of the region bounded by the curve y = x3, x = 1, x = 4 and the X-axis is ______
The area of the circle x2 + y2 = 16 is ______
The area of the region bounded by y2 = 25x, x = 1 and x = 2 the X axis is ______
Find area of the region bounded by the curve y = – 4x, the X-axis and the lines x = – 1 and x = 2
Find the area of the region bounded by the curve x = `sqrt(25 - y^2)`, the Y-axis lying in the first quadrant and the lines y = 0 and y = 5
The area of the region bounded by the curve y = 4x3 − 6x2 + 4x + 1 and the lines x = 1, x = 5 and X-axis is ____________.
Area enclosed between the curve y2(4 - x) = x3 and line x = 4 above X-axis is ______.
Area under the curve `y=sqrt(4x+1)` between x = 0 and x = 2 is ______.
The area of the region bounded by the curve y = x IxI, X-axis and the ordinates x = 2, x = –2 is ______.
The slope of a tangent to the curve y = 3x2 – x + 1 at (1, 3) is ______.
Find the area between the two curves (parabolas)
y2 = 7x and x2 = 7y.
The figure shows as triangle AOB and the parabola y = x2. The ratio of the area of the triangle AOB to the area of the region AOB of the parabola y = x2 is equal to ______.
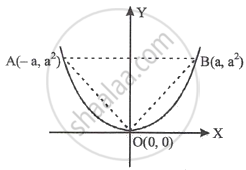
The area enclosed by the parabola x2 = 4y and its latus rectum is `8/(6m)` sq units. Then the value of m is ______.
