Question

Using integration find the area of the region {(x, y) : x2+y2⩽ 2ax, y2⩾ ax, x, y ⩾ 0}.

Answer 1

 

Given:

x²+y²≤2ax, y²≥ax, x, y≥0

⇒x²+y²−2ax≤0,  y²≥ax, x, y≥0

⇒x²+y²−2ax+a²−a²≤0,  y²≥ax, x, y≥0

⇒(x−a)²+y²≤a²,  y²≥ax, x, y≥0

To find the points of intersection of the circle [(x−a)²+y²=a²] and the parabola

[y²=ax],

we will substitute y²=ax in (x−a)²+y²=a².

(x−a)²+ax=a²

⇒x²+a²−2ax+ax=a²

⇒x(x−a)=0

⇒x=0, a

Therefore, the points of intersection are (0, 0), (a, a) and (a, −a).

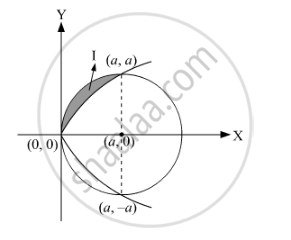
Now,

Area of the shaded region= I

Area of I from x=0 to x=a

`=[int_0^a(sqrt(a^2-(x-a^2)))dx-int_0^asqrt(axd)x]`

 Let x−a=t for the first part of the integral  `int_0^a(sqrt(a^2-(x-a^2)))dx`

⇒dx=dt

`:.A_I=int_(-a)^0sqrt(a^2-t^2)dt-2sqrta/3|x^(3/2)|_0^a`

`=|t/2sqrt(a^2-t^2)+1/2a^2sin^(-1)`

 `=0-(-(pia^2)/4)-(2a^2)/3`

 `A_I=(pi/4-2/3)a^2`

∴Area of the shaded region = `(pi/4-2/3)a^2`square units