Advertisements
Advertisements
Question
The area of the region bounded by y2 = 4x, the X-axis and the lines x = 1 and x = 4 is _______.
Solution
The area of the region bounded by y2 = 4x, the X-axis and the lines x = 1 and x = 4 is `underlinebb(28/3)` sq. units.
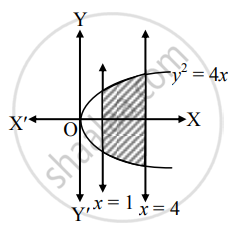
Required area = `2int_1^4y*dx`
= `2int_1^4 2sqrt(x)*dx`
= `2[x^(3/2)/(3/2)]_1^4`
= `2[(2x^(3/2))/(3)]_1^4`
Substituting the values we get
= `2 = ((2(4)^(3/2))/3 - (2(1)^(3/2))/3)`
= `4 (8/3 - 1/3)`
= `4 (7/3)`
= `28/3` sq. units.
APPEARS IN
RELATED QUESTIONS
Find the area of the smaller part of the circle x2 + y2 = a2 cut off by the line `x = a/sqrt2`
Find the area of the region bounded by the curve y2 = 4x and the line x = 3
Area of the region bounded by the curve y2 = 4x, y-axis and the line y = 3 is ______.
Using the method of integration find the area of the triangle ABC, coordinates of whose vertices are A(2, 0), B (4, 5) and C (6, 3).
Using the method of integration, find the area of the triangle ABC, coordinates of whose vertices are A (4 , 1), B (6, 6) and C (8, 4).
Find the area of the region bounded by the following curves, the X-axis and the given lines: y = `sqrt(16 - x^2)`, x = 0, x = 4
Find the area of the region bounded by the following curves, the X-axis and the given lines: 2y + x = 8, x = 2, x = 4
Fill in the blank :
Area of the region bounded by y = x4, x = 1, x = 5 and the X-axis is _______.
Using definite integration, area of the circle x2 + y2 = 49 is _______.
Solve the following :
Find the area of the region bounded by the curve y = x2 and the line y = 10.
Solve the following:
Find the area of the region bounded by the curve x2 = 25y, y = 1, y = 4 and the Y-axis.
Find area of the region bounded by the parabola x2 = 4y, the Y-axis lying in the first quadrant and the lines y = 3
If `int_0^(pi/2) log (cos x) "dx" = - pi/2 log 2,` then `int_0^(pi/2) log (cosec x)`dx = ?
Area bounded by the curve xy = 4, X-axis between x = 1, x = 5 is ______.
Equation of a common tangent to the circle, x2 + y2 – 6x = 0 and the parabola, y2 = 4x, is:
If a2 + b2 + c2 = – 2 and f(x) = `|(1 + a^2x, (1 + b^2)x, (1 + c^2)x),((1 + a^2)x, 1 + b^2x, (1 + c^2)x),((1 + a^2)x, (1 + b^2)x, 1 + c^2x)|` then f(x) is a polynomial of degree
The area included between the parabolas y2 = 4a(x +a) and y2 = 4b(x – a), b > a > 0, is
The area of the region bounded by the curve y = x2, x = 0, x = 3, and the X-axis is ______.
Area bounded by y = sec2x, x = `π/6`, x = `π/3` and x-axis is ______.
Find the area of the region lying in the first quadrant and bounded by y = 4x2, x = 0,y = 2 and y = 4.
