Advertisements
Advertisements
प्रश्न
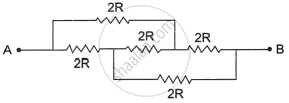
- Assertion (A): The equivalent resistance between points A and B in the given networks is 2R.
- Reason (R): All the resistors are connected in parallel.
पर्याय
Both Assertion (A) and Reason (R) are true and (R) is the correct explanation of (A).
Both Assertion (A) and Reason (R) are true and (R) is not the correct explanation of (A).
Assertion (A) is true and Reason (R) is false.
Assertion (A) is false and Reason (R) is also false.
उत्तर
Assertion (A) is true and Reason (R) is false.
Explanation:
The resistors in the following circuit are linked in both series and parallel configurations. We must simplify the circuit using the necessary criteria in order to determine the equivalent resistance between points A and B. We may reduce the circuit to a single equivalent resistor between locations A and B by applying the series and parallel rules to the resistors. The resulting equivalent resistance is:
Req = 2R
Therefore, the assertion (A) is correct, and the reason (R) is incorrect as well. All the resistors are not connected in parallel.
संबंधित प्रश्न
Two resistors R1 = 400Ω and R2 = 20 n are connected in parallel to a battery. If heating the power developed in R1 is 25 W. find the heating power developed in R2
Two heating elements of resistances R1 and R2 when operated at a constant supply of voltage, V, consume powers P1 and P2 respectively. Deduce the expressions for the power of their combination whey they are, in turn, connected in (i) series and (ii) parallel across the same voltage supply.
Suppose you have three resistors of 20 Ω, 50 Ω and 100 Ω. What minimum and maximum resistance can you obtain from these resistors?
A wire of resistance 15.0 Ω is bent to form a regular hexagon ABCDEFA. Find the equivalent resistance of the loop between the points (a) A and B (b) A and C and (c) Aand D.
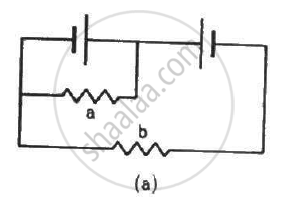
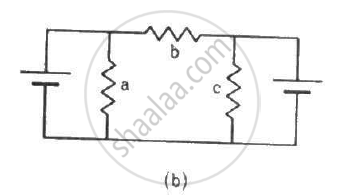
Each of the resistors shown in the figure has a resistance of 10 Ω and each of the batteries has an emf of 10 V. Find the currents flowing through the resistors a and bin the two circuits.
Two resistors R1= 60 Ω and R2 = 90Ω are connected in parallel. If electric power consumed by the resistor R1 is15 W, calculate the power consumed by the resistor R2.
The instantaneous values of emf and the current in a series ac circuit are-
E = Eo Sin ωt and I = Io sin (ωt+π/3) respectively, then it is ______.
Assertion (A): To increase the range of an ammeter, we must connect a suitable high resistance in series to it.
Reason (R): The ammeter with increased range should have high resistance.
Select the most appropriate answer from the options given below:
Eight identical cells, each of emf 2V and internal resistance 3 Ω, are connected in series to form a row. Six such rows are connected in parallel to form a battery. This battery is now connected to an external resistor R of resistance 6 Ω. Calculate:
- emf of the battery.
- internal resistance of the battery.
- current flowing through R.
