Advertisements
Advertisements
प्रश्न
A wire of resistance 15.0 Ω is bent to form a regular hexagon ABCDEFA. Find the equivalent resistance of the loop between the points (a) A and B (b) A and C and (c) Aand D.
उत्तर
(a) 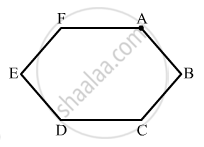
From the figure, it can be seen that between points A and B, the resistance of the first side of the hexagon will be in parallel with the total resistance of the other five sides.
The resistance of the first side can be calculated as shown below.
Resistance of the first leg = \[\frac{\text{Length of the that portion}}{\text{Total length}} \times R = \frac{\frac{1}{6}}{\frac{5}{6} + \frac{1}{6}} \times 15 = 15 \times \frac{1}{6}\]
Total resistance of the 5 legs = \[\frac{\frac{5}{6}}{\frac{1}{6} + \frac{5}{6}} \times 15 = \frac{5}{6} \times 15\]
∴ The effective resistance between the points A and B,
\[R_{eff} = \frac{\frac{15 \times 5}{6} \times \frac{15}{6}}{\frac{15 \times 5}{6} + \frac{15}{6}} = \frac{\frac{15 \times 5 \times 15}{6 \times 6}}{\frac{75 + 15}{6}}\]
\[ = \frac{15 \times 5 \times 15}{6 \times 90} = \frac{25}{12}\]
\[ = 2 . 08 \Omega\]
(b) From the figure, it can be seen that between points A and C, the resistance of the first two sides of the hexagon will be in parallel with the total resistance of the other four sides.
Resistance of the two legs = \[\frac{\text{Length of the that portion}}{\text{Total length}} \times R = \frac{\frac{2}{6}}{\frac{4}{6} + \frac{2}{6}} \times 15 = 15 \times \frac{2}{6}\]
Total resistance of the four legs = \[\frac{\frac{4}{6}}{\frac{2}{6} + \frac{4}{6}} \times 15 = \frac{4}{6} \times 15\]
∴ The effective resistance between the points A and C,
\[R_{eff} = \frac{\frac{15 \times 4}{6} \times \frac{15 \times 2}{6}}{\frac{15 \times 4}{6} + \frac{15 \times 2}{6}} = \frac{\frac{15 \times 4 \times 2 \times 15}{6 \times 6}}{\frac{60 + 30}{6}}\]
\[ = \frac{15 \times 2 \times 4 \times 15}{6 \times 90}\]
\[ = \frac{10}{3} = 3 . 33 \Omega\]
(c) From the figure, it can be seen that between points A and D, the resistance of the first three sides of the hexagon will be in parallel with the total resistance of the other three sides.
Resistance of the three legs = \[\frac{\text{Length of the that portion}}{\text{Total length}} \times R = \frac{\frac{3}{6}}{\frac{3}{6} + \frac{3}{6}} \times 15 = 15 \times \frac{3}{6}\]
∴ The effective resistance between the points A and D,
\[R_{eff} = \frac{\frac{15 \times 3}{6} \times \frac{15 \times 3}{6}}{\frac{15 \times 3}{6} + \frac{15 \times 3}{6}} = \frac{\frac{15 \times 3 \times 3 \times 15}{6 \times 6}}{\frac{90}{6}}\]
\[ = \frac{15 \times 3 \times 3 \times 15}{6 \times 90} = \frac{15}{4} = 3 . 75 \Omega\]
APPEARS IN
संबंधित प्रश्न
Two resistors R1 = 400Ω and R2 = 20 n are connected in parallel to a battery. If heating the power developed in R1 is 25 W. find the heating power developed in R2
A uniform wire of resistance 50 Ω is cut into 5 equal parts. These parts are now connected in parallel. The equivalent resistance of the combination is ______________ .
Which of the following quantities does not change when a resistor connected to a battery is heated due to the current?
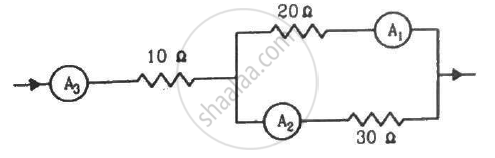
If the reading of the ammeter, A1 in the following figure is 2.4 A, what will be the readings of ammeters A2 and A3? Neglect the resistances of the ammeters.
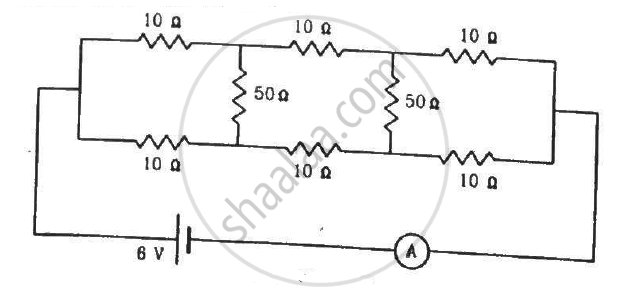
Find the current measured by the ammeter in the circuit shown in the figure.
The emf ε and the internal resistance r of the battery, shown in the figure, are 4.3 V and 1.0 Ω respectively. The external resistance R is 50 Ω. The resistances of the ammeter and voltmeter are 2.0 Ω and 200 Ω respectively. (a) Find the readings of the two meters. (b) The switch is thrown to the other side. What will be the readings of the two meters now?

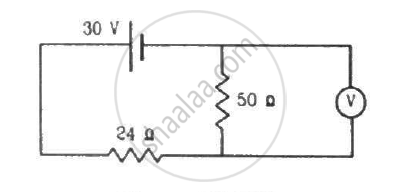
The voltmeter shown in the figure reads 18 V across the 50 Ω resistor. Find the resistance of the voltmeter.
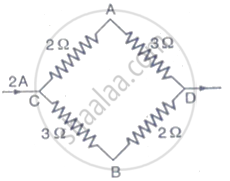
A current of 2 A flows in conductors as shown. The potential difference VA- VB will be ________.
An ammeter together with an unknown resistance in series is connected across two identical batteries each of emf 1.5 V. When the batteries are connected in series, the galvanometer records a current of 1A and when the batteries are in parallel, the current is 0.6A. Then the internal resistance of the battery is ______.
To get maximum current in a resistance of 3 ohms, one can use n rows of m cells (connected in series) connected in parallel. If the total number of cells is 24 and the internal resistance of a cell is 0.5 ohms then ______.
An electric current is passed through a circuit containing two wires of the same material, connected in parallel. If the lengths and radii of the wires are in the ratio of 3:2 and 2:3, then the ratio of the current passing through the wire will be ____________.
The instantaneous values of emf and the current in a series ac circuit are-
E = Eo Sin ωt and I = Io sin (ωt+π/3) respectively, then it is ______.
Three resistors having values R battery. Suppose R1 carries a current of 2.0 A, R ohms, and R3 dissipates 6.0 watts of power. Then the voltage across R is ______.
The equivalent resistance of resistors connected in series is always ______
Let there be n resistors R1............Rn with Rmax = max (R1......... Rn) and Rmin = min {R1..... Rn}. Show that when they are connected in parallel, the resultant resistance RP < R min and when they are connected in series, the resultant resistance RS > Rmax. Interpret the result physically.
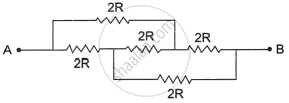
- Assertion (A): The equivalent resistance between points A and B in the given networks is 2R.
- Reason (R): All the resistors are connected in parallel.