Advertisements
Advertisements
Question
A wire of resistance 15.0 Ω is bent to form a regular hexagon ABCDEFA. Find the equivalent resistance of the loop between the points (a) A and B (b) A and C and (c) Aand D.
Solution
(a) 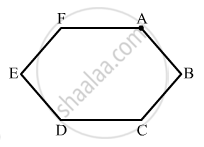
From the figure, it can be seen that between points A and B, the resistance of the first side of the hexagon will be in parallel with the total resistance of the other five sides.
The resistance of the first side can be calculated as shown below.
Resistance of the first leg = \[\frac{\text{Length of the that portion}}{\text{Total length}} \times R = \frac{\frac{1}{6}}{\frac{5}{6} + \frac{1}{6}} \times 15 = 15 \times \frac{1}{6}\]
Total resistance of the 5 legs = \[\frac{\frac{5}{6}}{\frac{1}{6} + \frac{5}{6}} \times 15 = \frac{5}{6} \times 15\]
∴ The effective resistance between the points A and B,
\[R_{eff} = \frac{\frac{15 \times 5}{6} \times \frac{15}{6}}{\frac{15 \times 5}{6} + \frac{15}{6}} = \frac{\frac{15 \times 5 \times 15}{6 \times 6}}{\frac{75 + 15}{6}}\]
\[ = \frac{15 \times 5 \times 15}{6 \times 90} = \frac{25}{12}\]
\[ = 2 . 08 \Omega\]
(b) From the figure, it can be seen that between points A and C, the resistance of the first two sides of the hexagon will be in parallel with the total resistance of the other four sides.
Resistance of the two legs = \[\frac{\text{Length of the that portion}}{\text{Total length}} \times R = \frac{\frac{2}{6}}{\frac{4}{6} + \frac{2}{6}} \times 15 = 15 \times \frac{2}{6}\]
Total resistance of the four legs = \[\frac{\frac{4}{6}}{\frac{2}{6} + \frac{4}{6}} \times 15 = \frac{4}{6} \times 15\]
∴ The effective resistance between the points A and C,
\[R_{eff} = \frac{\frac{15 \times 4}{6} \times \frac{15 \times 2}{6}}{\frac{15 \times 4}{6} + \frac{15 \times 2}{6}} = \frac{\frac{15 \times 4 \times 2 \times 15}{6 \times 6}}{\frac{60 + 30}{6}}\]
\[ = \frac{15 \times 2 \times 4 \times 15}{6 \times 90}\]
\[ = \frac{10}{3} = 3 . 33 \Omega\]
(c) From the figure, it can be seen that between points A and D, the resistance of the first three sides of the hexagon will be in parallel with the total resistance of the other three sides.
Resistance of the three legs = \[\frac{\text{Length of the that portion}}{\text{Total length}} \times R = \frac{\frac{3}{6}}{\frac{3}{6} + \frac{3}{6}} \times 15 = 15 \times \frac{3}{6}\]
∴ The effective resistance between the points A and D,
\[R_{eff} = \frac{\frac{15 \times 3}{6} \times \frac{15 \times 3}{6}}{\frac{15 \times 3}{6} + \frac{15 \times 3}{6}} = \frac{\frac{15 \times 3 \times 3 \times 15}{6 \times 6}}{\frac{90}{6}}\]
\[ = \frac{15 \times 3 \times 3 \times 15}{6 \times 90} = \frac{15}{4} = 3 . 75 \Omega\]
APPEARS IN
RELATED QUESTIONS
Three resistors 1 Ω, 2 Ω, and 3 Ω are combined in series. What is the total resistance of the combination?
Two heating elements of resistances R1 and R2 when operated at a constant supply of voltage, V, consume powers P1 and P2 respectively. Deduce the expressions for the power of their combination whey they are, in turn, connected in (i) series and (ii) parallel across the same voltage supply.
A uniform wire of resistance 50 Ω is cut into 5 equal parts. These parts are now connected in parallel. The equivalent resistance of the combination is ______________ .
Suppose you have three resistors of 20 Ω, 50 Ω and 100 Ω. What minimum and maximum resistance can you obtain from these resistors?
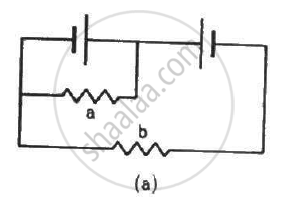
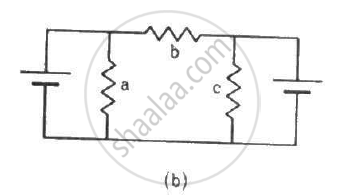
Each of the resistors shown in the figure has a resistance of 10 Ω and each of the batteries has an emf of 10 V. Find the currents flowing through the resistors a and bin the two circuits.
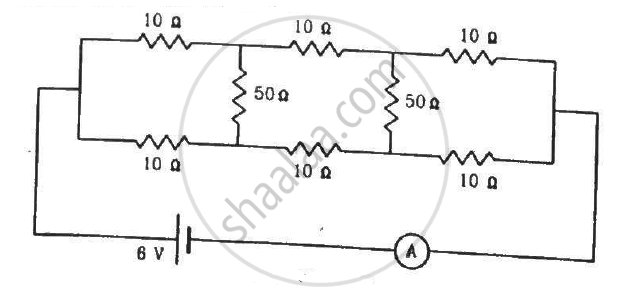
Find the current measured by the ammeter in the circuit shown in the figure.
The emf ε and the internal resistance r of the battery, shown in the figure, are 4.3 V and 1.0 Ω respectively. The external resistance R is 50 Ω. The resistances of the ammeter and voltmeter are 2.0 Ω and 200 Ω respectively. (a) Find the readings of the two meters. (b) The switch is thrown to the other side. What will be the readings of the two meters now?

Two resistors of equal resistances are joined in series and a current is passed through the combination. Neglect any variation in resistance as the temperature changes. In a given time interval,
(a) equal amounts of thermal energy must be produced in the resistors
(b) unequal amounts of thermal energy may be produced
(c) the temperature must rise equally in the resistors
(d) the temperature may rise equally in the resistors
Two voltameters, one with a solution of silver salt and the other with a trivalent-metal salt, are connected in series and a current of 2 A is maintained for 1.50 hours. It is found that 1.00 g of the trivalent metal is deposited. (a) What is the atomic weight of the trivalent metal?
(b) How much silver is deposited during this period? Atomic weight of silver is 107.9 g mol−1.
Two resistors R1= 60 Ω and R2 = 90Ω are connected in parallel. If electric power consumed by the resistor R1 is15 W, calculate the power consumed by the resistor R2.
An ammeter together with an unknown resistance in series is connected across two identical batteries each of emf 1.5 V. When the batteries are connected in series, the galvanometer records a current of 1A and when the batteries are in parallel, the current is 0.6A. Then the internal resistance of the battery is ______.
Combine three resistors 5 Q, 4.5 Q and 3 Q in such a way that the total resistance of this combination is maximum ______.
In parallel combination of n cells, we obtain ______.
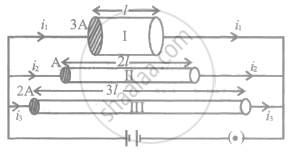
The figure shows three conductors I, II and III of same material, different lengths l, 2l and 3l and of different areas of cross-sections 3A, A and 2A respectively. Arrange them in the increasing order of current drawn from the battery.
A condenses having a capacity 2.0 µF is charged to 200 V and the plates of the capacitor are connected to a resistance wire. The heat produce in it will be:-
Let there be n resistors R1............Rn with Rmax = max (R1......... Rn) and Rmin = min {R1..... Rn}. Show that when they are connected in parallel, the resultant resistance RP < R min and when they are connected in series, the resultant resistance RS > Rmax. Interpret the result physically.
Eight identical cells, each of emf 2V and internal resistance 3 Ω, are connected in series to form a row. Six such rows are connected in parallel to form a battery. This battery is now connected to an external resistor R of resistance 6 Ω. Calculate:
- emf of the battery.
- internal resistance of the battery.
- current flowing through R.
Three bulbs B1 (230V, 40W), B2 (230V, 60W) and B3 (230V, 100W) are connected in series to a 230V supply. Which bulb glows the brightest?
