Advertisements
Advertisements
प्रश्न
If the reading of the ammeter, A1 in the following figure is 2.4 A, what will be the readings of ammeters A2 and A3? Neglect the resistances of the ammeters.
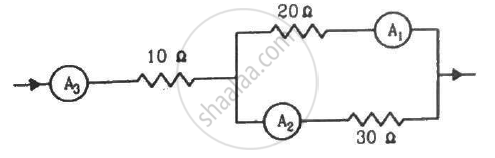
उत्तर
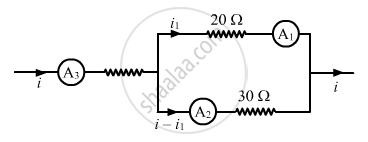
Given: i1 = 2.4 A
Since the 20 Ω and 30 Ω resistors are connected in parallel, the voltage across them will be the same.
From the figure,
\[20 i_1 = 30\left( i - i_1 \right)\]
\[ \Rightarrow 50 i_1 = 30i\]
\[ \Rightarrow i = \frac{50 i_1}{30} = 3 . 99 = 4 A\]
∴ The reading of ammeter A3 = i = 4 A
The reading of ammeter A2 = i - i1 = 1.6 A
APPEARS IN
संबंधित प्रश्न
A bulb is made using two filaments. A switch selects whether the filaments are used individually or in parallel. When used with a 15 V battery, the bulb can be operated at 5 W, 10 W or 15 W. What should be the resistances of the filaments?
A wire of resistance 15.0 Ω is bent to form a regular hexagon ABCDEFA. Find the equivalent resistance of the loop between the points (a) A and B (b) A and C and (c) Aand D.
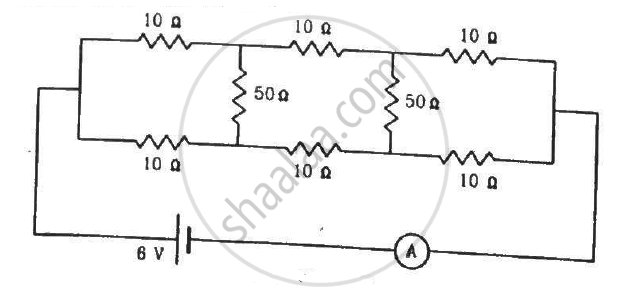
Find the current measured by the ammeter in the circuit shown in the figure.
The emf ε and the internal resistance r of the battery, shown in the figure, are 4.3 V and 1.0 Ω respectively. The external resistance R is 50 Ω. The resistances of the ammeter and voltmeter are 2.0 Ω and 200 Ω respectively. (a) Find the readings of the two meters. (b) The switch is thrown to the other side. What will be the readings of the two meters now?

A voltmeter coil has resistance 50.0 Ω and a resistor of 1.15 kΩ is connected in series. It can read potential differences up to 12 volts. If this same coil is used to construct an ammeter that can measure currents up to 2.0 A, what should be the resistance of the shunt used?
Two voltameters, one with a solution of silver salt and the other with a trivalent-metal salt, are connected in series and a current of 2 A is maintained for 1.50 hours. It is found that 1.00 g of the trivalent metal is deposited. (a) What is the atomic weight of the trivalent metal?
(b) How much silver is deposited during this period? Atomic weight of silver is 107.9 g mol−1.
A solenoid L and a resistor R are connected in series to a battery, through a switch. When the switch is put on, current I flowing through it varies with time t as shown in which of the graphs given below:
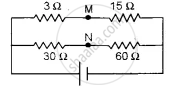
How much resistance should be connected to 15 Ω resistor shown in the circuit in figure below so that the points M and N are at the same potential:
To get maximum current in a resistance of 3 ohms, one can use n rows of m cells (connected in series) connected in parallel. If the total number of cells is 24 and the internal resistance of a cell is 0.5 ohms then ______.
In parallel combination of n cells, we obtain ______.
An electric current is passed through a circuit containing two wires of the same material, connected in parallel. If the lengths and radii of the wires are in the ratio of 3:2 and 2:3, then the ratio of the current passing through the wire will be ____________.
If two resistors of resistances R1 = (4 ± 0.5) Ω and R2 = (16 ± 0.5) Ω are connected in series. The eqivalent resistance with the limits of percentage error is ______.
Two electric lamps of each 40 watt are connected in series. The power consumed by the combination will be
The effective resistance of a parallel connection that consists of four wires of equal length, equal area of cross-section and the same material is 0.25 Ω. What will be the effective resistance if they are connected in series?
The effective resistance of a parallel connection that consists of four wires of equal length, equal area of cross-section and same material is 0.25 Ω. What will be the effective resistance if they are connected in series?
An electric cable of copper has just one wire of radius 9 mm. Its resistance is 14Ω. If this single copper wire of the cable is replaced by seven identical well insulated copper wires each of radius 3 mm connected in parallel, then the new resistance of the combination will be:
Eight identical cells, each of emf 2V and internal resistance 3 Ω, are connected in series to form a row. Six such rows are connected in parallel to form a battery. This battery is now connected to an external resistor R of resistance 6 Ω. Calculate:
- emf of the battery.
- internal resistance of the battery.
- current flowing through R.
