Advertisements
Advertisements
प्रश्न
Can all the angles of a quadrilateral be acute angles? Give reason for your answer.
उत्तर
We know that, sum of all angles of a quadrilateral = 360°
So atleast one angle should be obtuse angle.
Hence, all the four angles of a quadrilateral cannot be acute angles.
APPEARS IN
संबंधित प्रश्न
The angles of a quadrilateral are in the ratio 3 : 5 : 9 : 13 Find all the angles of the quadrilateral.
Two opposite angles of a parallelogram are (3x – 2)° and (50 – x)°. Find the measure of each angle of the parallelogram .
If an angle of a parallelogram is two-third of its adjacent angle, find the angles of the parallelogram .
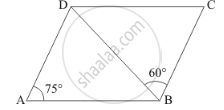
In Fig. below, ABCD is a parallelogram in which ∠DAB = 75° and ∠DBC = 60°. Compute
∠CDB and ∠ADB.
If PQRS is a square, then write the measure of ∠SRP.
If the angles of a quadrilateral are in the ratio 3 : 5 : 9 : 13, then find the measure of the smallest angle.
If an angle of a parallelogram is two-third of its adjacent angle, the smallest angle of the parallelogram is
In the following figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. Prove that AD = 2CD.

The angles of a quadrilateral are in the ratio 1 : 2 : 3 : 4. The smallest angle is ______.
The angles P, Q, R and S of a quadrilateral are in the ratio 1:3:7:9. Then PQRS is a ______.
