Advertisements
Advertisements
प्रश्न
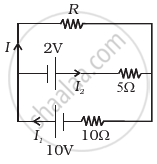
Determine the current in each branch of the network shown in figure.

उत्तर
Current flowing through various branches of the circuit is represented in the given figure.
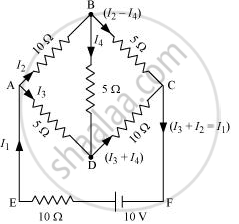
I1 = Current flowing through the outer circuit
I2 = Current flowing through branch AB
I3 = Current flowing through branch AD
I2 − I4 = Current flowing through branch BC
I3 + I4 = Current flowing through branch CD
I4 = Current flowing through branch BD
For the closed-circuit ABDA, the potential is zero i.e.,
10 I2 + 5 I4 − 5 I3 = 0
2 I2 + I4 − I3 = 0
I3 = 2 I2 + I4 ....(1)
For the closed-circuit BCDB, the potential is zero i.e.,
5(I2 − I4) − 10(I3 + I4) − 5I4 = 0
5 I2 + 5 I4 − 10 I3 − 10 I4 − 5 I4 = 0
5 I2 − 10 I3 − 20 I4 = 0
I2 = 2 I3 + 4 I4 .....(2)
For the closed circuit ABCFEA, potential is zero i.e.,
−10 + 10 (I1) + 10 (I2) + 5(I2 − I4) = 0
10 = 15 I2 + 10 I1 − 5 I4
3 I2 + 2 I1 − I4 = 2 ....(3)
From equations (1) and (2), we obtain
I3 = 2(2 I3 + 4 I4) + I4
I3 = 4 I3 + 8 I4 + I4
−3 I3 = 9 I4
−3 I4 = + I3 ....(4)
Putting equation (4) in equation (1), we obtain
I3 = 2 I2 + I4
− 4 I4 = 2 I2
I2 = −2 I4 ....(5)
It is evident from the given figure that,
I1 = I3 + I2 ....(6)
Putting equation (6) in equation (1), we obtain
3 I2 + 2(I3 + I2) − I4 = 2
5 I2 + 2 I3 − I4 = 2 .....(7)
Putting equations (4) and (5) in equation (7), we obtain
5(−2 I4) + 2(−3 I4) − I4 = 2
− 10 I4 − 6 I4 − I4 = 2
17 I4 = −2
I4 = `(-2)/17"A"`
Equation (4) reduces to
I3 = −3(I4)
= `-3((-2)/17)`
= `6/17"A"`
I2 = −2(I4)
= `-2((-2)/17)`
= `4/17"A"`
`"I"_2 - "I"_4 = 4/17 - ((-2)/17)`
= `6/17"A"`
`"I"_3 + "I"_4 = 6/17 + ((-2)/17)`
= `4/17 "A"`
I1 = I3 + I2
= `6/17 + 4/17`
= `10/17"A"`
Therefore, current in branch AB = `4/17"A"`
In branch BC = `6/17"A"`
In branch CD = `(-4)/17"A"`
In branch AD = `6/17"A"`
In branch BD = `((-2)/17)"A"`
Total current = `4/17 + 6/17 + (-4)/17 + 6/17 + (-2)/17`
= `10/17"A"`
APPEARS IN
संबंधित प्रश्न
Kirchhoff's voltage law and current law are respectively in accordance with the conservation of .................................. .
- charge and momentum
- charge and energy
- energy and charge
- energy and momentum
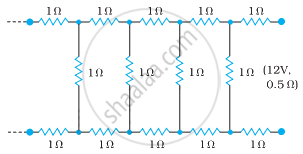
Determine the current drawn from a 12 V supply with internal resistance 0.5 Ω by the infinite network shown in the figure. Each resistor has 1 Ω resistance.
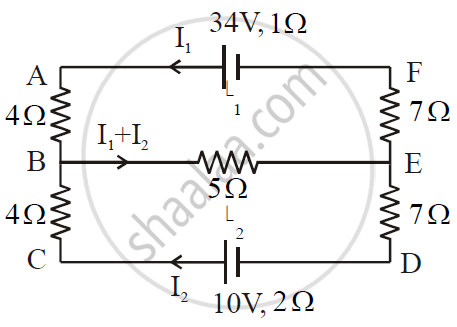
ε1 and ε2 are two batteries having emf of 34V and 10V respectively and internal resistance of 1Ω and 2Ω respectively. They are connected as shown in the figure below. Using Kirchhoff’s Laws of electrical networks, calculate the currents I1 and I2.
State Kirchhoff's rules and explain on what basis they are justified.
Find the circuit in the three resistors shown in the figure.
Twelve wires, each of equal resistance r, are joined to form a cube, as shown in the figure. Find the equivalent resistance between the diagonally-opposite points a and f.

A capacitor of capacitance 8.0 μF is connected to a battery of emf 6.0 V through a resistance of 24 Ω. Find the current in the circuit (a) just after the connections are made and (b) one time constant after the connections are made.
Solve the following question.
Using Kirchhoff’s rules, calculate the current through the 40 Ω and 20 Ω resistors in the following circuit.

Twelve wires each having a resistance of 3 Ω are connected to form a cubical network. A battery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of this network. Determine its equivalent resistance and the current along each edge of the cube.
State Kirchhoff ’s voltage rule.
Explain the determination of unknown resistance using meter bridge.
How the emf of two cells are compared using potentiometer?
A copper wire of 10-6 m2 area of cross-section, carries a current of 2 A. If the number of electrons per cubic meter is 8 × 1028, calculate the current density and average drift velocity.
The Kirchhoff's second law (ΣiR = ΣE), where the symbols have their usual meanings, is based on ______.
What are the advantages of the null-point method in a Wheatstone bridge? What additional measurements would be required to calculate `R_(unknown)` by any other method?
Two cells of voltage 10V and 2V and internal resistances 10Ω and 5Ω respectively, are connected in parallel with the positive end of 10V battery connected to negative pole of 2V battery (Figure). Find the effective voltage and effective resistance of the combination.
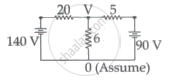
The value of current in the 6Ω resistance is ______.
A 6-volt battery is connected to the terminals of a three-metre-long wire of uniform thickness and resistance of 100 ohms. The difference of potential between two points on the wire separated by a distance of 50 cm will be ______.
