Advertisements
Advertisements
प्रश्न
दो समरूप त्रिभुजों के क्षेत्रफल 36 cm2 और 100 cm2 हैं। यदि बड़े त्रिभुज की एक भुजा की लंबाई 20 cm है, तो उस भुजा के संगत छोटे त्रिभुज की भुजा की लंबाई ज्ञात कीजिए।
उत्तर
दिया गया है, छोटे त्रिभुज का क्षेत्रफल = 36 cm2
और बड़े त्रिभुज का क्षेत्रफल = 100 cm2
साथ ही, बड़े त्रिभुज की एक भुजा की लंबाई = 20 cm
माना छोटे त्रिभुज की संगत भुजा की लंबाई = x cm
समरूप त्रिभुज के क्षेत्रफल के गुण से,
`("ar(बड़ा त्रिभुज)")/("ar(छोटा त्रिभुज)") = ("बड़े त्रिभुज की भुजा")^2/("छोटे त्रिभुज की भुजा")^2`
⇒ `100/36 = (20)^2/x^2`
⇒ x2 = `((20)^2 xx 36)/100`
⇒ x2 = `(400 xx 36)/100` = 144
∴ x = `sqrt(144)` = 12 cm
अतः, छोटे त्रिभुज की संगत भुजा की लंबाई 12 सेमी है।
APPEARS IN
संबंधित प्रश्न
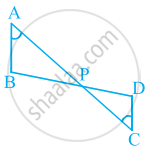
समलंब ABCD, जिसमें AB || DC है, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं। दो त्रिभजों की समरूपता कसौटी का प्रयोग करते हुए, दर्शाइए कि `"OA"/"OC" = "OB"/"OD"` है।
आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:

ΔPDC ∼ ΔBEC
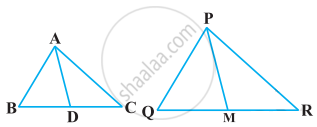
एक त्रिभुज ABC की भुजाएँ AB और BC तथा माध्यिका AD एक अन्य त्रिभुज PQR की क्रमशः भुजाओं PQ और QR तथा माध्यिका PM के समानुपाती है (देखिए आकृति)। दर्शाइए कि ∆ABC ∼ ∆PQR है।
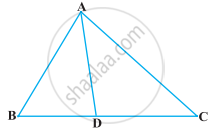
एक त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि ∠ADC = ∠BAC है। दर्शाइए कि CA2 = CB.CD है।
आकृति में त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि `"BD"/"CD" = "AB"/"AC"` है। सिद्ध कीजिए कि AD, कोण BAC का समद्विभाजक है।
ΔABC ~ ΔDFE, ∠A = 30°, ∠C = 50°, AB = 5 cm, AC = 8 cm और DF = 7.5 cm दिया हुआ है। तब, निम्नलिखित ______ सत्य है।
APQR की भुजा QR पर कोई बिंदु D इस प्रकार है कि PD ⊥ QR है। क्या ΔPQD ~ ΔRPD कहना सही होगा? क्यो?
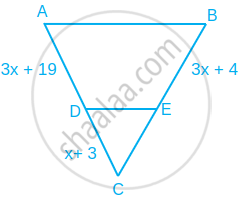
x का वह मान ज्ञात कीजिए. जिसके लिए आकृति में DE || AB हो।
यदि ∆ABC ~ ∆DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm और FD = 12 cm है, तो ∆ABC का परिमाप ज्ञात कीजिए।
आकृति में, यदि ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm और CP = 4 cm है, तो PD और CD की लंबाइयाँ ज्ञात कीजिए।