Advertisements
Advertisements
प्रश्न
During an experiment, an ideal gas is found to obey an additional law pV2 = constant. The gas is initially at a temperature T and volume V. Find the temperature when it expands to a volume 2V.
Use R = 8.3 J K-1 mol-1
उत्तर
Applying equation of state of an ideal gas, we get
PV = nRT
⇒ P = \[\frac{nRT}{V} . . . 1 \]
Taking differentials, we get
⇒ PdV + VdP = nRdT . . . 2
Applying the additional law, we get
PV2 = c
V2 dP + 2VPdV = 0
⇒ VdP + 2PdV = 0 . . . 3
Subtracting eq. (3) from eq. (2) , we get
PdV = -nRdT
⇒ dV = \[\ {-}\frac{nR}{P}dT \]
Now ,
⇒ dV = \[\ {-}\frac{V}{T}dT \] [From eq. (1}]
⇒ \[\frac{dV}{V} = {-}\frac{dT}{T} \]
Integrating between T2 and T1 , we get
⇒ \[\int\limits_{V_1}^{2V} = {-}\int\limits_{T_1}^{T_2}\]
⇒ ln( 2V) - ln(V) = ln (T1) - ln (T2)
⇒ `ln ((2V)/V)` = `ln ((T_1)/(T_2))`
⇒ `T_2 = T_1/2`
APPEARS IN
संबंधित प्रश्न
Which of the following parameters is the same for molecules of all gases at a given temperature?
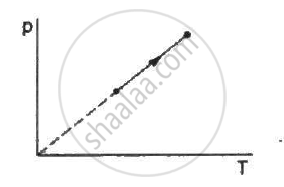
The process on an ideal gas, shown in figure, is
Which of the following quantities is the same for all ideal gases at the same temperature?
(a) The kinetic energy of 1 mole
(b) The kinetic energy of 1 g
(c) The number of molecules in 1 mole
(d) The number of molecules in 1 g
The temperature and pressure at Simla are 15.0°C and 72.0 cm of mercury and at Kalka these are 35.0°C and 76.0 cm of mercury. Find the ratio of air density at Kalka to the air density at Simla.
Use R=8.314J K-1 mol-1
An ideal gas is trapped between a mercury column and the closed-end of a narrow vertical tube of uniform base containing the column. The upper end of the tube is open to the atmosphere. The atmospheric pressure equals 76 cm of mercury. The lengths of the mercury column and the trapped air column are 20 cm and 43 cm respectively. What will be the length of the air column when the tube is tilted slowly in a vertical plane through an angle of 60°? Assume the temperature to remain constant.
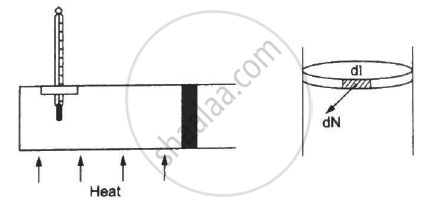
Figure shows a cylindrical tube of radius 5 cm and length 20 cm. It is closed by a tight-fitting cork. The friction coefficient between the cork and the tube is 0.20. The tube contains an ideal gas at a pressure of 1 atm and a temperature of 300 K. The tube is slowly heated and it is found that the cork pops out when the temperature reaches 600 K. Let dN denote the magnitude of the normal contact force exerted by a small length dlof the cork along the periphery (see the figure). Assuming that the temperature of the gas is uniform at any instant, calculate `(dN)/(dt)`.
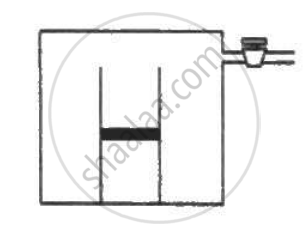
An ideal gas is kept in a long cylindrical vessel fitted with a frictionless piston of cross-sectional area 10 cm2 and weight 1 kg in figure. The vessel itself is kept in a big chamber containing air at atmospheric pressure 100 kPa. The length of the gas column is 20 cm. If the chamber is now completely evacuated by an exhaust pump, what will be the length of the gas column? Assume the temperature to remain constant throughout the process.
Using figure, find the boiling point of methyl alcohol at 1 atm (760 mm of mercury) and at 0.5 atm.

A glass contains some water at room temperature 20°C. Refrigerated water is added to it slowly. when the temperature of the glass reaches 10°C, small droplets condense on the outer surface. Calculate the relative humidity in the room. The boiling point of water at a pressure of 17.5 mm of mercury is 20°C and at 8.9 mm of mercury it is 10°C.
An adiabatic cylindrical tube of cross-sectional area 1 cm2 is closed at one end and fitted with a piston at the other end. The tube contains 0.03 g of an ideal gas. At 1 atm pressure and at the temperature of the surrounding, the length of the gas column is 40 cm. The piston is suddenly pulled out to double the length of the column. The pressure of the gas falls to 0.355 atm. Find the speed of sound in the gas at atmospheric temperature.
Answer in brief:
Show that rms velocity of an oxygen molecule is `sqrt2` times that of a sulfur dioxide molecule at S.T.P.
If the density of oxygen is 1.44 kg/m3 at a pressure of 105 N/m2, find the root mean square velocity of oxygen molecules.
Energy is emitted from a hole in an electric furnace at the rate of 20 W when the temperature of the furnace is 727°C. What is the area of the hole? (Take Stefan’s constant σ to be 5.7 × 10-8 Js-1 m-2K-4.)
The number of degrees of freedom, for the vibrational motion of a polyatomic molecule, depends on the ______
Calculate the energy radiated in one minute by a blackbody of surface area 200 cm2 at 127 °C (σ = 5.7 x 10-8 J m-2 s-1 K-4)
If the density of nitrogen is 1.25 kg/m3 at a pressure of 105 Pa, find the root mean square velocity of nitrogen molecules.
Assuming the expression for the pressure exerted by the gas on the wall of the container, it can be shown that pressure is ______.
A gas mixture consists of molecules of types A, B and C with masses mA > mB > mC. Rank the three types of molecules in decreasing order of average K.E.
Consider a rectangular block of wood moving with a velocity v0 in a gas at temperature T and mass density ρ. Assume the velocity is along x-axis and the area of cross-section of the block perpendicular to v0 is A. Show that the drag force on the block is `4ρAv_0 sqrt((KT)/m)`, where m is the mass of the gas molecule.
Show that the average energy per molecule is proportional to the absolute temperature T of the gas.
