Advertisements
Advertisements
प्रश्न
एक रोड रोलर की लंबाई 2.1 मीटर तथा उस का व्यास 1.4 मीटर है। किसी मैदान को समतल करने के लिए रोलर को 500 फेरे लगाने पड़ते हैं। तो रोलर ने कितनी वर्गमीटर जमीन समतल की ? 7 रुपये प्रति वर्गमी की दर से कितना खर्च आएगा?
उत्तर
रोड रोलर की त्रिज्या, r = `1.4/2` = 0.7 मी
रोड रोलर की लंबाई, h = 2.1 मी
∴ रोड रोलर दवारा एक फेरे में समतल किए गए मैदान का क्षेत्रफल = रोड रोलर का वक्र पृष्ठफल
= 2πrh
= `2 xx 22/7 xx 0.7 xx 2.1`
= 9.24 मी2
रोड रोलर दवारा 500 फेरों में समतल किए गए मैदान का क्षेत्रफल = 500 × एक फेरे में समतल किए गए मैदान का क्षेत्रफल
= 500 × 9.24
= 4620 मी2
मैदान को समतल करने का दर = ₹ 7 मी2
∴ मैदान को समतल करने का खर्च = रोड रोलर दवारा समतल किए गए मैदान का क्षेत्रफल × मैदान को समतल करने का दर
= 4620 × 7
= ₹ 32,340
इस प्रकार, रोड रोलर ने 4620 वर्ग मीटर जमीन समतल की। जमीन को समतल करने का खर्च ₹ 32,340 है।
APPEARS IN
संबंधित प्रश्न
किसी लंब वृत्ताकार बेलन के आधार की त्रिज्या 5 सेमी तथा ऊँचाई क्रमश: 40 सेमी हो तो उसका संपूर्ण पृष्ठफल ज्ञात कीजिए |
नीचे दिए गए बहुवैकल्पिक प्रश्न में से उचित विकल्प चुनकर लिखिए।
5 सेमी त्रिज्या वाले किसी लंबवृत्ताकार बेलन का वक्रपृष्ठफल 440 सेमी2 हो तो उस लंबवृत्ताकार बेलन की ऊँचाई कितनी होगी?
नीचे दिए गए बहुवैकल्पिक प्रश्न में से उचित विकल्प चुनकर लिखिए।
किसी शंकु को पिघलाकर उसके आधार की त्रिज्या के बराबर त्रिज्या वाला लंबवृत्ताकार बेलन बनाया गया। यदि लंबवृत्ताकार बेलन की ऊँचाई 5 सेमी हो तो शंकु की ऊँचाई कितनी होगी?
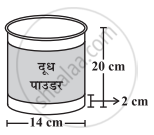
एक कंपनी अपने दूध पाउडर को ऐसे बेलनाकार बर्तनों में पैक करती है जिनका व्यास 14 cm और ऊँचाई 20 cm है। कंपनी बर्तन के पृष्ठ के चारों ओर एक लेबल लगाती है (जैसा कि आकृति में दर्शया गया है)। यदि यह लेबल बर्तन के तल और शीर्ष दोनों से 2 cm की दूरी पर चिपकाया जाता है तो लेबल का क्षेत्रफल क्या है?
यदि एक बेलन की त्रिज्या दोगुनी कर दी जाए और ऊँचाई आधी कर दी जाए, तो इसका वक्र पृष्ठीय क्षेत्रफल ______ होगा।
दो बेलनों की त्रिज्याएँ 2 : 3 के अनुपात में हैं तथा उनकी ऊँचाईयों का अनुपात 5 : 3 है। उनके आयतनों का अनुपात है
यदि एक बेलन की त्रिज्या दुगुनी कर दी जाए तथा उसके वक्र पृष्ठीय क्षेत्रफल में कोई परिवर्तन न किया जाए, तो उसकी ऊँचाई अवश्य ही आधी हो जाएगी।
एक बेलन और एक लंब वृत्तीय शंकु के समान आधार और समान ऊँचाई हैं। बेलन का आयतन शंकु के आयतन का तिगुना हैं।
2.5 m लंबे और 1.75 m त्रिज्या वाले एक बेलनाकार रोलर (roller) को जब सड़क पर रोल किया गया तो पाया गया कि उसने 5500 m2 के क्षेत्रफल को तय कर लिया है। रोलर ने कितने चक्कर लगा लिए थे?
वृत्ताकार लंब बेलन का वक्र पृष्ठफल 1980 सेमी2 है और आधार की त्रिज्या 15 सेमी तो उस वृत्ताकार लंब बेलन की ऊँचाई ज्ञात कीजिए। (π = `22/7`)
