Advertisements
Advertisements
प्रश्न
एक सम अष्टभुज के प्रत्येक कोण की माप ज्ञात कीजिए।
उत्तर
अष्टभुज में भुजाओं की संख्या (n) = 8
अब, एक नियमित अष्टभुज के आंतरिक कोणों का योग = (n – 2) × 180°
= (8 – 2) × 180°
= 6 × 180°
= 1080°
चूंकि, अष्टकोण नियमित है, प्रत्येक कोण का माप = `1080^circ/8` = 135°
APPEARS IN
संबंधित प्रश्न
उत्तल चतुर्भुज के कोणों के मापों का योगफल क्या है? यदि चतुर्भुज उत्तल न हो तो क्या ये गुण लागू होगा ? (एक चतुर्भुज बनाइए जो उत्तल ना हो और प्रयास कीजिए।)
तालिका की जांच कीजिए : (प्रत्येक आकृति को त्रिभुजों में बाँटिए और कोणों का योगफल ज्ञात कीजिए।)
| आकृति | 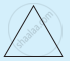 |
 |
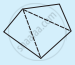 |
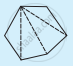 |
| भुजा | 3 | 4 | 5 | 6 |
| कोणों का योगफल | 180° | 2 × 180° = (4 - 2) × 180° | 3 × 180° = (5 - 2) × 180° | 4 × 180° = (6 - 2) × 180° |
एक बहुभुज के कोणों के योग के बारे में आप क्या कह सकते हैं, जिसकी भुजाओं की संख्या निम्नलिखित हो।
- 7
- 8
- 10
- n
एक सम बहु भुज का नाम बताइए जिसमें 6 भुजाएँ हों।
एक सम बहुभुज के प्रत्येक बाह्य कोण का माप ज्ञात कीजिए जिसकी 15 भुजाएँ हो।
किसी सम बहुभुज में अधिक से अधिक कितने अंश का बाह्य कोण संभव है ?
इन आकृतियों में दिखाए गए कोणों को देखो। क्या तुम इनमें अंतर देख पा रहे हो?
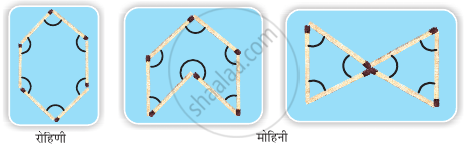
एक अवतल चतुर्भुज के कोणों का योग होता है –
निम्न में कौन एक सम बहुभुज का बहिष्कोण नहीं हो सकता?
प्रत्येक अंतःकोण 135∘ वाले एक समबहुभुज की भुजाओं की संख्या है –
एक अवतल चतुर्भुज के ______ कोण की माप 180∘ से अधिक होती है।
