Advertisements
Advertisements
प्रश्न
Evaluate the following
sin2 30° + sin2 45° + sin2 60° + sin2 90°
उत्तर
sin2 30° + sin2 45° + sin2 60° + sin2 90° .....(1)
`sin 30^@ = 1/2 sin 45^@ = 1/sqrt2`
`sin 60^@ = sqrt3/2 sin 90^@ = 1`
By substituting above values in (i), we get
`= [1/2]^2 + [1/sqrt2]^2 + [sqrt3/2]^2 + [1]^2`
`= 1/4 + 1/2 + 3/4 + 1 => (1 + 3)/4 + (1 + 2)/2`
`=> 1 + 3/2 = (2 + 3)/2 = 5/2`
APPEARS IN
संबंधित प्रश्न
If sin θ = `12/13`, Find `(sin^2 θ - cos^2 θ)/(2sin θ cos θ) × 1/(tan^2 θ)`.
If `tan θ = 20/21` show that `(1 - sin theta + cos theta)/(1 + sin theta + cos theta) = 3/7`
Evaluate the Following
(cos 0° + sin 45° + sin 30°)(sin 90° − cos 45° + cos 60°)
Find the value of x in the following :
cos 2x = cos 60° cos 30° + sin 60° sin 30°
If cos A + cos² A = 1, then sin² A + sin4 A is equal to ______.
3 sin² 20° – 2 tan² 45° + 3 sin² 70° is equal to ______.
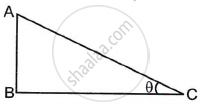
In ΔABC, ∠ABC = 90° and ∠ACB = θ. Then write the ratios of sin θ and tan θ from the figure.
Let tan9° = `(1 - sqrt((sqrt(5)k)/m))k` where k = `sqrt(5) + 1` then m is equal to ______.
(3 sin2 30° – 4 cos2 60°) is equal to ______.
In ΔBC, right angled at C, if tan A = `8/7`, then the value of cot B is ______.