Advertisements
Advertisements
प्रश्न
Explain why there is no atmosphere on moon.
उत्तर
The moon has a small gravitational force (pull) and hence, the escape velocity is small. The value of escape velocity for the moon is 4.6 km/s.
As the moon is in the proximity of the earth as seen from the sun, the moon has the same amount of heat per unit area as that of the earth.
The air molecules have a large range of speeds. Even though the rms speed of the air molecules is smaller than the escape velocity on the moon, a significant number of molecules have speeds greater than escape velocity and they escape.
Now, the rest of the molecules arrange the speed distribution for the equilibrium temperature. Again a significant number of molecules escape as their speed exceeds the escape speed. Hence, over a long time, the moon has lost most of its atmosphere.
At 300 K, `V_(rms) = sqrt((3kT)/m)`
= `sqrt((3 xx 1.38 xx 10^-23 xx 300)/(7.3 xx 10^-26)`
= 1.7 km/s
Vesc for moon = 4.6 km/s ......[Vesc = escape velocity]
APPEARS IN
संबंधित प्रश्न
Can we define the temperature of (a) vacuum, (b) a single molecule?
A gas is kept in an enclosure. The pressure of the gas is reduced by pumping out some gas. Will the temperature of the gas decrease by Charles's low?
Which of the following quantities is the same for all ideal gases at the same temperature?
(a) The kinetic energy of 1 mole
(b) The kinetic energy of 1 g
(c) The number of molecules in 1 mole
(d) The number of molecules in 1 g
Calculate the energy radiated in one minute by a blackbody of surface area 200 cm2 at 127 °C (σ = 5.7 x 10-8 J m-2 s-1 K-4)
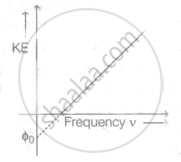
The graph of kinetic energy against the frequency v of incident light is as shown in the figure. The slope of the graph and intercept on X-axis respectively are ______.
The average K.E. of hydrogen molecules at 27° C is E. The average K.E. at 627° C is ____________.
The molecules of a given mass of a gas have root mean square speeds of 100 ms−1 at 27°C and 1.00 atmospheric pressure. What will be the root mean square speeds of the molecules of the gas at 127°C and 2.0 atmospheric pressure?
Consider a rectangular block of wood moving with a velocity v0 in a gas at temperature T and mass density ρ. Assume the velocity is along x-axis and the area of cross-section of the block perpendicular to v0 is A. Show that the drag force on the block is `4ρAv_0 sqrt((KT)/m)`, where m is the mass of the gas molecule.
When a particle oscillates simple harmonically, its kinetic energy varies periodically. If frequency of the particle is n, then the frequency of the kinetic energy is ______.
According to the kinetic theory of gases, at a given temperature, molecules of all gases have the same ______.
