Advertisements
Advertisements
प्रश्न
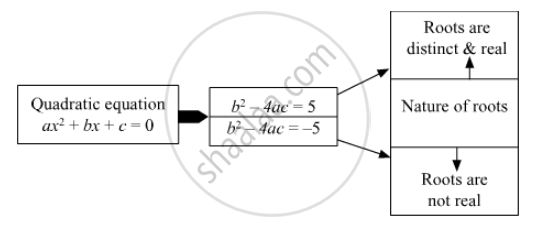
Fill in the gaps and complete.
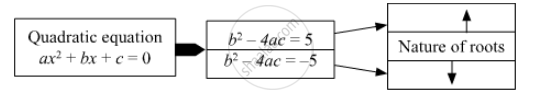
उत्तर
APPEARS IN
संबंधित प्रश्न
Solve the following quadratic equation for x: `4x^2 + 4bx – (a^2 – b^2) = 0`
Find the roots of the following quadratic equations, if they exist, by the method of completing the square `4x^2 + 4sqrt3x + 3 = 0`
Find the roots of the quadratic equations 2x2 + x – 4 = 0 by applying the quadratic formula.
The difference of squares of two numbers is 180. The square of the smaller number is 8 times the larger number. Find the two numbers
Find the roots of the following quadratic equations (if they exist) by the method of completing the square.
x2 - 4ax + 4a2 - b2 = 0
`4x^2+4bx-(a^2-b^2)=0`
`x^2-(sqrt2+1)x+sqrt2=0`
Solve the following quadratic equation by completing the square method.
9y2 – 12y + 2 = 0
Solve the following quadratic equation by completing the square method.
5x2 = 4x + 7
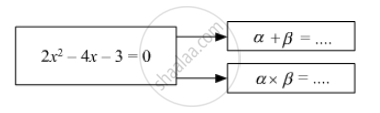
Fill in the gaps and complete.
If α, β are roots of quadratic equation,
Find the value of discriminant.
x2 + 7x – 1 = 0
Determine the nature of roots of the following quadratic equation.
m2 + 2m + 9 = 0
Sum of the roots of a quadratic equation is double their product. Find k if equation x2 – 4kx + k + 3 = 0
α, β are roots of y2 – 2y –7 = 0 find,
α2 + β2
α, β are roots of y2 – 2y –7 = 0 find,
α3 + β3
The difference of two natural numbers is 3 and the difference of their reciprocals is \[\frac{3}{28}\].Find the numbers.
In a flight of 600 km, an aircraft was slowed due to bad weather. Its average speed for the trip was reduced by 200 km/hr and the time of the flight increased by 30 minutes. Find the scheduled duration of the flight.
One year ago, a man was 8 times as old as his son. Now his age is equal to the square of his son’s age. Their present ages are:
Find the value of x, if 3x – 7 × 4x – 4 = 768.
Find the value of x, if `5^(x - 3) xx 5^(2x – 8)` = 625.
